题目内容
【题目】如图,将![]() 沿弦
沿弦![]() 折叠,使折叠后的劣弧
折叠,使折叠后的劣弧![]() 恰好经过圆心O,连接
恰好经过圆心O,连接![]() 并延长交
并延长交![]() 于点C,点P是优弧
于点C,点P是优弧![]() 上的动点,连接
上的动点,连接![]() .
.
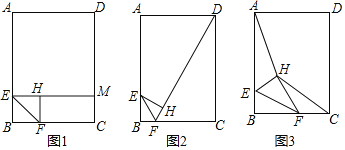
(1)如图,用尺规面出折叠后的劣弧![]() 所在圆的圆心
所在圆的圆心![]() ,并求出
,并求出![]() 的度数;
的度数;
(2)如图,若![]() 是
是![]() 的切线,
的切线,![]() ,求线段
,求线段![]() 的长;
的长;
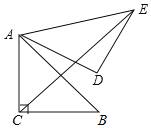
(3)如图,连接![]() ,过点B作
,过点B作![]() 的重线,交
的重线,交![]() 的延长线于点D,求证:
的延长线于点D,求证:![]() .
.

【答案】(1)图见解析,![]() =60°;(2)AP=4
=60°;(2)AP=4![]() ;(3)见解析.
;(3)见解析.
【解析】
![]() 分别作AO,AB的垂直平分线,其交点即为劣弧
分别作AO,AB的垂直平分线,其交点即为劣弧![]() 所在圆的圆心
所在圆的圆心![]() ,由作图的过程可知AO,OB,
,由作图的过程可知AO,OB,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]()
![]() 的半径,可证△AO
的半径,可证△AO![]() 与△BO
与△BO![]() 均为等边三角形,点
均为等边三角形,点![]() 在
在![]() 上,则可求出
上,则可求出![]() ,根据圆周角定理可求出
,根据圆周角定理可求出![]() 的度数;
的度数;![]() 连接
连接![]() ,证明
,证明![]() 为
为![]() 的直径,则
的直径,则![]() ,在
,在![]() 中利用勾股定理可求出AP的长;
中利用勾股定理可求出AP的长;![]() 延长AP至M,使
延长AP至M,使![]() ,连接CM,证明
,连接CM,证明![]() ∽
∽![]() ,可证明
,可证明![]() ,进一步可证明
,进一步可证明![]() .
.
解:![]() 如图1,分别作AO,AB的垂直平分线,其交点即为劣弧
如图1,分别作AO,AB的垂直平分线,其交点即为劣弧![]() 所在圆的圆心
所在圆的圆心![]() ,
,
连接A![]() ,B
,B![]() ,OB,
,OB,![]() ,OB,
,OB,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的半径,
的半径,
∴AO=BO=![]() =
=![]() =
=![]() ,
,
∴△AO![]() 与△BO
与△BO![]() 均为等边三角形,点
均为等边三角形,点![]() 在
在![]() 上,
上,
∴![]() ,
,![]() ,
,
∴∠AOB=∠AO![]() +∠BO
+∠BO![]() =120°,
=120°,![]() ;
;![]() 如图2,连接
如图2,连接![]() ,
,
![]() 是
是![]() 的切线,
的切线,
∴AP⊥![]() ,
,
∴![]() ,
,
∴![]() 为圆O的直径,
为圆O的直径,![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ;
;![]() 如图3,延长AP至M,使
如图3,延长AP至M,使![]() ,连接CM,
,连接CM,
![]() 为
为![]() 的直径,
的直径,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由![]() 知,
知,![]() ,
,![]() ,
,![]() ,
,
即![]() ,
,![]() ,
,![]() ∽
∽![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

练习册系列答案
相关题目