Question

已知抛物线y＝ax²＋bx＋c与x轴交于A、B两点，与y轴交于点C，其中点B在x轴的正半轴上，点C在y轴的正半轴上，线段OB、OC的长（OB<OC）是方程x²－10x＋16＝0的两个根，且抛物线的对称轴是直线x＝－2．

（1）求此抛物线的解析式；

（2）连接AC、BC，若点E是线段AB上的一个动点（与点A、点B不重合），过点E作EF∥AC交BC于点F，连接CE，设AE的长为m，△CEF的面积为S，求S与m之间的函数关系式，并写出自变量m的取值范围；

（3）在（2）的基础上试说明S是否存在最大值，若存在，请求出S的最大值，并求出此时点E的坐标，判断此时△BCE的形状；若不存在，请说明理由。

 

Answer 1

【答案】

（1）所求抛物线的表达式为:  （2）

（3）为等腰三角形，理由点E和点B关于直线OC轴对称，所以CE=CB

【解析】

试题分析：（1）解方程x²-10x+16=0得x₁=2，x₂=8，

由题意得:A（-6，0），C（0，8），B（2，0）

∵点C（0，8）在抛物线y=ax²+bx+c的图象上，∴c=8，

将A（-6，0）、B（2，0）代入表达式，得，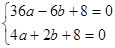

解得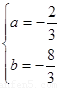       

∴所求抛物线的表达式为:    

(2)由 A（-6，0），C（0，8），B（2，0）得：AB=8，OC=8，OA=6，

∵AE="m," ∴BE="8-m."   

在Rt △AOC中，由勾股定理得：

  

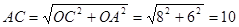
设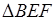中BE边上的高为h.

∵EF//AC

∽

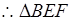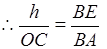,即，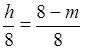  

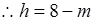
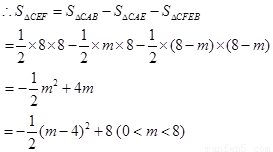
(3) 由（2）知，S存在最大值，最大值为8平方单位， 

此时，m=4，所以点E坐标为（-2,0）， 

点E和点B关于直线OC轴对称；为等腰三角形。

考点：抛物线，等腰三角形，相似三角形

点评：本题考查抛物线，等腰三角形，要求考生会用待定系数法求函数的解析式，掌握抛物线的性质，熟悉等腰三角形的判定方法，会判定两个三角形相似