Question

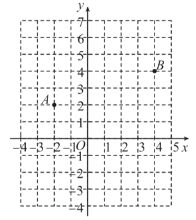
【题目】如图:在平面直角坐标系中，点.

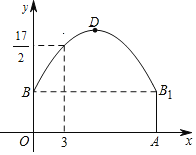
(1)尺规作图:求作过三点的圆;

(2)设过三点的圆的圆心为M，利用网格，求点M的坐标;

(3)若直线与相交，直接写出的取值范围.

Answer 1

【答案】（1）见解析；（2）M(1,3)；（3）

【解析】

(1) 作OA和OB的垂直平分线，交点即为圆心，据此作圆即可；

(2)AB的中点即为圆心M，由此可解；

(3)求出半径，即可知直线与相切时a的值，由此可得相交时的取值范围.

解：(1) 如图即为所要求作的过三点的圆；

作OA和OB的垂直平分线，交点即为圆心，作圆即可.

(2) 由图可知， ∠AOB=，所以AB是所求作圆的直径，

因为AB中点的坐标为(1,3),

即所求圆心M的坐标是(1,3).

（3）由圆心M和圆上任意点可求出半径r=AM=BM=，

∴当a=1-或1+时，直线与相切，

∴当 时，直线与相交.