Question

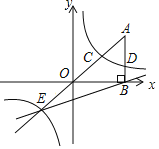
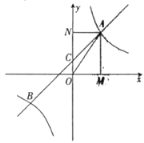
【题目】如图，在平面直角坐标系中，一次函数的图象与反比例函数的图象交于第一、三象限内的、两点，与轴交于点，过点作轴于点，作轴于点，，，点的坐标为．

(1)求四边形的周长和面积．

(2)求该反比例函数和一次函数的解析式．

Answer 1

【答案】(1) 四边形的周长为10，面积为6；(2) ；

【解析】

（1）利用三角函数求出AM的长，即可求得周长和面积;

（2）由(1)可求A的坐标,于是可求反比例解析式,然后求B坐标,求直线解析式即可得到答案；

(1)∵轴，

∴．

在中，，

∴．

∵轴，轴，

∴四边形是矩形，

∴四边形的周长，

四边形的面积．

(2)由(1)可知，，

∴点的坐标为．

把点代入，得，

解得，

∴反比例函数的解析式为．

把点代入，可得，

∴点的坐标为．

把、代入一次函数，可得

解得

∴一次函数的解析式为．