题目内容
如图⊙O是2×2正方形网格中的一个最大内切圆，则sinα=（ ）分析：先根据圆周角定理求出∠A=α，再根据勾股定理求出AB的长，由sin∠A=sinα=
即可得出结论．
| BC |
| AB |
解答：
解：∵∠A及α是同弧所对的圆周角，
∴∠A=α，
∵⊙O是2×2正方形网格，
∴AC=4，BC=2，
∴AB=
=
=2
，
∴sin∠A=sinα=
=
=
．
故选A．
解：∵∠A及α是同弧所对的圆周角，∴∠A=α，
∵⊙O是2×2正方形网格，
∴AC=4，BC=2，
∴AB=
| AC2+BC2 |
| 42+22 |
| 5 |
∴sin∠A=sinα=
| BC |
| AB |
| 2 | ||
2
|
| ||
| 5 |
故选A．
点评：本题考查的是圆周角定理及勾股定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．
练习册系列答案
相关题目
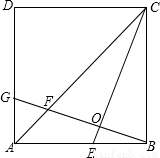
24、如图，在正方ABCD中，E是AB边上任一点，BG⊥CE，垂足为O，交AC于点F，交AD于点G．
27、如图1是具有2000多年历史的古城扬州市区内的几个旅游景点分布示意图．（图中每个小正方形的边长均为1个单位长度）
如图的大正方行格板是由81个1平方厘米的小正方形铺成，B，C是两个格点．若请你在其它的格点中标出一点A，使得△ABC的面积恰等于3平方厘米，则这样的A点共有（ ）个．
的位置：平山堂________、荷花池________，竹西公园________．