题目内容
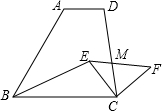
 如图,直角梯形BCDF中,∠BCD=90°,BC∥FD,CA⊥BD于A,点E在FD上,且BF=BE,∠BEA=∠ACD,下列结论:
如图,直角梯形BCDF中,∠BCD=90°,BC∥FD,CA⊥BD于A,点E在FD上,且BF=BE,∠BEA=∠ACD,下列结论:
①∠ACD=∠CBD;②∠FBC+∠CBE=180°;③DE+DF=2BC;④BC=BE.
其中正确的个数为
- A.1个
- B.2个
- C.3个
- D.4个
D
分析:根据∠ACD+∠BCA=90°和∠CBD+∠BCA=90°即可推出∠ACD=∠CBD;根据∠FBC+∠F=180°和∠F=∠BEF=∠CBE推出即可;过B作BH⊥DF于H,求出BC=DH,根据等腰三角形性质求出FH=HE,即可得出DE+DF=2BC;证△BAC∽△BCD和△BEA∽△BDE,得出比例式,即可得出BC2=BE2=BA×BD,即可得出BC=BE.
解答: 解:∵∠BCD=90°,
解:∵∠BCD=90°,
∴∠ACD+∠BCA=90°,
∵CA⊥BD,
∴∠BAC=90°,
∴∠CBD+∠BCA=90°,
∴∠ACD=∠CBD,
∴①正确;
∵BC∥FD,
∴∠CBE=∠BEF,∠F+∠FBC=180°,
∵BF=BE,
∴∠F=∠BEF,
∴∠FBC+∠CBE=180°,
∴②正确;
过点B作BH⊥EF于点H,
∵BF=BE,
∴EH=FH,
∵直角梯形BCDF中,∠BCD=90°,BC∥FD,
∴四边形BCDH是矩形,
∴BC=DH=EH+DE,
∴DE+DF=DH+FH+DE=DH+DH=BC+BC=2BC,
∴③正确;
∵∠BCD=90°,CA⊥BD,
∴∠CAB=∠CAD=∠BCD=90°,
∴∠CBD+∠CDB=90°,∠DCA+∠CDB=90°,
∴∠DCA=∠CBD,
∵BC∥DF,
∴∠CBD=∠BDE,
∵∠AEB=∠DCA,
∴∠BDE=∠BEA,
∵∠EBA=∠DBA,
∴△BEA∽△BDE,
∴ =
= ,
,
∴BE2BA×BD,
∵∠CBA=∠CBD,∠CAB=∠DCB,
∴△BAC∽△BCD,
∴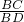 =
=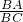 ,
,
∴BC2=BA×BD,
∴BE2=BC2,
∴BE=BC,∴④正确;
故选D.
点评:此题考查了梯形的性质、全等三角形的判定与性质、平行线分线段成比例定理以及三角函数的定义.此题难度适中,注意掌握数形结合思想与转化思想的应用.
分析:根据∠ACD+∠BCA=90°和∠CBD+∠BCA=90°即可推出∠ACD=∠CBD;根据∠FBC+∠F=180°和∠F=∠BEF=∠CBE推出即可;过B作BH⊥DF于H,求出BC=DH,根据等腰三角形性质求出FH=HE,即可得出DE+DF=2BC;证△BAC∽△BCD和△BEA∽△BDE,得出比例式,即可得出BC2=BE2=BA×BD,即可得出BC=BE.
解答:
 解:∵∠BCD=90°,
解:∵∠BCD=90°,∴∠ACD+∠BCA=90°,
∵CA⊥BD,
∴∠BAC=90°,
∴∠CBD+∠BCA=90°,
∴∠ACD=∠CBD,
∴①正确;
∵BC∥FD,
∴∠CBE=∠BEF,∠F+∠FBC=180°,
∵BF=BE,
∴∠F=∠BEF,
∴∠FBC+∠CBE=180°,
∴②正确;
过点B作BH⊥EF于点H,
∵BF=BE,
∴EH=FH,
∵直角梯形BCDF中,∠BCD=90°,BC∥FD,
∴四边形BCDH是矩形,
∴BC=DH=EH+DE,
∴DE+DF=DH+FH+DE=DH+DH=BC+BC=2BC,
∴③正确;

∵∠BCD=90°,CA⊥BD,
∴∠CAB=∠CAD=∠BCD=90°,
∴∠CBD+∠CDB=90°,∠DCA+∠CDB=90°,
∴∠DCA=∠CBD,
∵BC∥DF,
∴∠CBD=∠BDE,
∵∠AEB=∠DCA,
∴∠BDE=∠BEA,
∵∠EBA=∠DBA,
∴△BEA∽△BDE,
∴
 =
= ,
,∴BE2BA×BD,
∵∠CBA=∠CBD,∠CAB=∠DCB,
∴△BAC∽△BCD,
∴
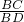 =
=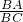 ,
,∴BC2=BA×BD,
∴BE2=BC2,
∴BE=BC,∴④正确;
故选D.
点评:此题考查了梯形的性质、全等三角形的判定与性质、平行线分线段成比例定理以及三角函数的定义.此题难度适中,注意掌握数形结合思想与转化思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,直角梯形ABCD中,∠BCD=90°,AD∥BC,BC=CD,E为梯形内一点,且∠BEC=90°,将△BEC绕C点旋转90°使B与D重合,得到△DCF,连EF交CD于M.已知BC=5,CF=3,则DM:MC的值为
如图,直角梯形ABCD中,∠BCD=90°,AD∥BC,BC=CD,E为梯形内一点,且∠BEC=90°,将△BEC绕C点旋转90°使B与D重合,得到△DCF,连EF交CD于M.已知BC=5,CF=3,则DM:MC的值为 20、如图,直角梯形ABCD中,∠A=90°,∠B=45°,底边AB=5,高AD=3,点E由B沿折线BCD向点D移动,EM⊥AB于M,EN⊥AD于N,设BM=x,矩形AMEN的面积为y,那么y与x之间的函数关系的图象大致是( )
20、如图,直角梯形ABCD中,∠A=90°,∠B=45°,底边AB=5,高AD=3,点E由B沿折线BCD向点D移动,EM⊥AB于M,EN⊥AD于N,设BM=x,矩形AMEN的面积为y,那么y与x之间的函数关系的图象大致是( ) 如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2.
如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2.
 如图,直角梯形BCDF中,∠BCD=90°,BC∥FD,CA⊥BD于A,点E在FD上,且BF=BE,∠BEA=∠ACD,下列结论:
如图,直角梯形BCDF中,∠BCD=90°,BC∥FD,CA⊥BD于A,点E在FD上,且BF=BE,∠BEA=∠ACD,下列结论: