题目内容
有一张矩形纸片ABCD,已知AB=2,AD=5.把这张纸片折叠,使点A落在边BC上的点E处,折痕为MN,MN交AB于M,交AD于N.
(1)若BE=
| 2 |
(2)点E在BC上运动时,设BE=x,AN=y,试求y关于x的函数解析式,并写出x的取值范围;
(3)连接DE,是否存在这样的点E,使得△AME与△DNE相似?若存在,请求出这时BE的长;若不存在,请说明理由.
分析:(1)根据折叠的性质,折叠前后线段相等,即AM=ME,再由勾股定理求得AM=
.
(2)仿(1)可求AM=
.又根据折叠的性质,可证△AMN∽△BEA,得
=
,推出y=
,定义域为:5-
≤x≤2.
(3)可用分析法:若△AME与△DNE相似,可推出DN=NE=NA=
,进而取得BE=1.
| 3 |
| 2 |
(2)仿(1)可求AM=
| 4+x2 |
| 4 |
| AN |
| AB |
| AM |
| BE |
| x2+4 |
| 2x |
| 21 |
(3)可用分析法:若△AME与△DNE相似,可推出DN=NE=NA=
| 5 |
| 2 |
解答:解:(1)画出正确的图形.(折痕MN必须与AB、AD相交)
设AM=t,则ME=t,MB=2-t,由BM2+BE2=ME2,得t=
,即AM=
.

(2)如上图(a),仿(1)得,AM=
.
由△AMN∽△BEA,得
=
,推出y=
,
∵0<x≤2,0<y≤5,
x的取值范围为:5-
≤x≤2.
(3)如上图(b),若△AME与△DNE相似,不难得∠DNE=∠AME.
又因为AM=ME,所以DN=NE=NA=
,所以
=
,
解得:x=1或x=4.
又∵5-
≤x≤2,故x=1.
或者由∠DEN=∠AEM,得∠AED=90°,
推出△ABE∽△ECD,
从而得BE=1.
设AM=t,则ME=t,MB=2-t,由BM2+BE2=ME2,得t=
| 3 |
| 2 |
| 3 |
| 2 |

(2)如上图(a),仿(1)得,AM=
| 4+x2 |
| 4 |
由△AMN∽△BEA,得
| AN |
| AB |
| AM |
| BE |
| x2+4 |
| 2x |
∵0<x≤2,0<y≤5,
x的取值范围为:5-
| 21 |
(3)如上图(b),若△AME与△DNE相似,不难得∠DNE=∠AME.
又因为AM=ME,所以DN=NE=NA=
| 5 |
| 2 |
| x2+4 |
| 2x |
| 5 |
| 2 |
解得:x=1或x=4.
又∵5-
| 21 |
或者由∠DEN=∠AEM,得∠AED=90°,
推出△ABE∽△ECD,
从而得BE=1.
点评:本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后线段相等.以及相似三角形的判定和勾股定理的运用,是一道综合性较强的题.

练习册系列答案
相关题目
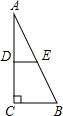 如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )
如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( ) 如图,在一张△ABC纸片中, ∠C=90°, ∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一
如图,在一张△ABC纸片中, ∠C=90°, ∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一




 = ;
= ; 




 = ;
= ; 