Question

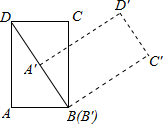如图，在计算机的白色屏幕上有一个矩形刷ABCD，AB=1，AD=

3

，以B为中心，按顺时针方向转到A′B′C′D′的位置，则这个画刷着色的面积的值是（　　）（注解：所谓画刷，是屏幕上的一个矩形块，它在屏幕上移动或转动时，它扫过的部位将改变颜色．）

• A．

  3

  +

  2

  3

  π
• B．π
• C．

  3

  +π
• D．2π-

  3

Answer 1

分析：先根据矩形的性质和勾股定理得到BD=

AB2+AD2

=2，则∠ADB=30°，∠ABD=60°，根据旋转的性质得到BC′=

3

，D′C′=1，∠DBD′=60°，然后利用这个画刷着色的面积=S_△BAD+S_扇形BDD′+S_△BD′C′和扇形的面积公式进行计算．

解答：解：∵AB=1，AD=

3

，四边形ABCD为矩形，
∴BD=

AB2+AD2

=2，
∴∠ADB=30°，∠ABD=60°，
∴∠DBC=30°，
∵以B为中心，按顺时针方向转到A′B′C′D′的位置，
∴BC′=

3

，D′C′=1，∠DBD′=60°，
∴这个画刷着色的面积=S_△BAD+S_扇形BDD′+S_△BD′C′
=

1

2

×1×

3

+

60•π•22

360

+

1

2

×1×

3

=

3

+

2

3

π．
故选A．

点评：本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角．也考查了勾股定理和矩形的性质以及扇形的面积公式．