题目内容
5．已知x4-5x3+ax2+bx+c能被（x-1）2整除，试求（a+b+c）2的值．分析 由于x4-5x3+ax2+bx+c能被（x-1）2整除，即1是方程x4-5x3+ax2+bx+c的一个根，把x=1代入x4-5x3+ax2+bx+c=0，得到关于a、b、c的三元一次方程，求得a+b+c的结果，即可得到（a+b+c）2的值．
解答 解：∵x4-5x3+ax2+bx+c能被（x-1）2整除，
即1是方程x4-5x3+ax2+bx+c的一个根，把x=1代入x4-5x3+ax2+bx+c=0，得
1-5+a+b+c=0，则a+b+c=4，
（a+b+c）2=42=16．
故（a+b+c）2的值是16．
点评 本题主要考查了整式乘除法与因式分解的关系及求代数式的值的方法，属于竞赛题型，有一定难度．本题的关键是能够通过整式乘除法与因式分解的关系得出x4-5x3+ax2+bx+c含有因式（x-1）2，从而可知1是方程x3+ax2+bx+c=0的一个根，从而求出（a+b+c）2的值．
练习册系列答案
相关题目
16．按如图所示的方法折纸，下面结论正确的个数（ ）
①∠2=90°；②∠1=∠AEC；③△ABE∽△ECF；④∠BAE=∠3．
①∠2=90°；②∠1=∠AEC；③△ABE∽△ECF；④∠BAE=∠3．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
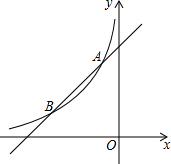如图，一次函数y1=x+6与反比例函数y2=$\frac{k}{x}$（x＜0）的图象相交于点A、B，其中点A的坐标是（-2，4）．
某射击小组进行射击练习，教练将该小组成员的某次射击成绩绘制成统计图（如图），则这组成绩的众数是7．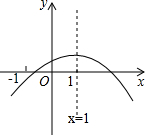
已知二次函数y=ax2+bx+c（a≠0）的图象如图，以下结论：
14．“一方有难，八方支援．”在某次捐款中某校师生共捐款13500元，把13500用科学记数法表示为（ ）
| A． | 1.35×106 | B． | 13.5×105 | C． | 1.35×104 | D． | 13.5×104 |