题目内容
已知(x2+y2-3)(x2+y2+1)=12,求x2+y2的值.
考点:换元法解一元二次方程
专题:
分析:先设z=x2+y2,则原方程变形为z2-2z-15=0,运用因式分解法解得z1=5,z2=-3,即可求得x2+y2的值.
解答:
解:设z=x2+y2,
原方程变形为(z-3)(z+1)=12,
整理,得z2-2z-15=0,
因式分解,得(z-5)(z+3)=0,
解得z1=5,z2=-3,
∵x2+y2≥0,
∴x2+y2的值为5.
原方程变形为(z-3)(z+1)=12,
整理,得z2-2z-15=0,
因式分解,得(z-5)(z+3)=0,
解得z1=5,z2=-3,
∵x2+y2≥0,
∴x2+y2的值为5.
点评:本题考查了换元法解一元二次方程:我们常用的是整体换元法,是在已知或者未知中,某个代数式几次出现,而用一个字母来代替它从而简化问题,当然有时候要通过变形才能发现.把一些形式复杂的方程通过换元的方法变成一元二次方程,从而达到降次的目的.

练习册系列答案
相关题目
如果AD是△ABC的中线,那么下列结论一定成立的有( )
①BD=CD;②AB=AC;③S△ABD=
S△ABC.
①BD=CD;②AB=AC;③S△ABD=
| 1 |
| 2 |
| A、3个 | B、2个 | C、1个 | D、0个 |
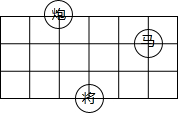 如图,象棋盘(部分)中,若“马”位置用(0,0)表示,“炮”的位置用(-3,1)表示,则“将”的位置表示为( )
如图,象棋盘(部分)中,若“马”位置用(0,0)表示,“炮”的位置用(-3,1)表示,则“将”的位置表示为( )| A、(0,0) |
| B、(-2,-2) |
| C、(0,-2) |
| D、(-2,-3) |
下列方程中,属于一元二次方程的是( )
| A、(x+6)2=16 | ||
| B、x2+3x=16+x2 | ||
| C、xy=16 | ||
D、x2-
|
下列运算正确的是( )
| A、a3•a3=2a3 |
| B、a3+a3=a6 |
| C、(-2a2)3=-8a6 |
| D、a6÷a3=a2 |
下列运算中,正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、|1-
|