��Ŀ����
��֪����x2+px+8����x2-3x+q���Ľ���в���x2���x3��.
��1����p��q��ֵ.
��2��x2-2px+3q�Ƿ�����ȫƽ��ʽ������ǣ��뽫��ֽ���ʽ��������ǣ���˵������.
���𰸡���1��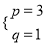 ����2��x2-2px+3q������ȫƽ��ʽ.���ɼ�����.
����2��x2-2px+3q������ȫƽ��ʽ.���ɼ�����.
�����������������(1)չ��,������x2���x3��ϵ��Ϊ0.
(2)�ѣ�1���н��۴��룬��������ȫƽ����ʽ.
���������
�⣺��1��ԭʽ=x4+��-3+p��x3+��q-3p+8��x2+��pq-24��x+8q.
�߽���в���x2���x3��� 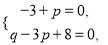
���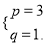
��2��x2-2px+3q������ȫƽ��ʽ.�������£�
��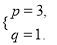 ����x2-2px+3q����x2-2px+3q=x2-6x+3.
����x2-2px+3q����x2-2px+3q=x2-6x+3.
��x2-6x+9����ȫƽ��ʽ����x2-6x+3������ȫƽ��ʽ.
�����͡������
��������
23
������ijͬѧ�Զ���ʽ��x2-4x+2����x2-4x+6��+4��ʽ�ֽ�Ĺ���.
��������
��x2-4x=y��
��ԭʽ=��y+2����y+6��+4����һ����
=y2+8y+16���ڶ�����
=��y+4��2����������
=��x2-4x+4��2�����IJ���
����������⣺
��1����ͬѧ�ڶ�������������������ʽ�ֽ�ķ����ǣ� ��
A.��ȡ����ʽ B.ƽ���ʽ C.�����͵���ȫƽ����ʽ D.���������ȫƽ����ʽ
��2����ͬѧ��ʽ�ֽ�Ľ���Ƿף�������ס������ס���.�������ף���ֱ��д����ʽ�ֽ���������
��3������ģ�����Ϸ������ԶԶ���ʽ��x2-2x����x2-2x+2��+1������ʽ�ֽ�.
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�

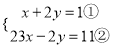 ��������������(2)
��������������(2) 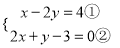
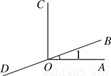
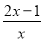 ���£�1��
���£�1��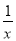 ���Ľ����________ ��
���Ľ����________ ��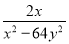 ��
��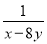 ��ֵΪ��������
��ֵΪ��������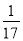 B.
B. 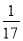 C.
C. 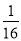 D.
D. 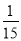
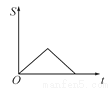 B.
B. 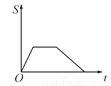 C.
C. 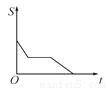 D.
D.