题目内容
1．
如图，有一张直角三角形纸片，两直角边长AC=6cm，BC=8cm，将△ABC折叠，使点B与点A重合，折痕为DE，则CD等于（ ）| A． | $\frac{25}{4}$cm | B． | $\frac{22}{3}$cm | C． | $\frac{7}{4}$cm | D． | $\frac{5}{3}$cm |
分析 根据折叠的性质得DA=DB，设CD=xcm，则BD=AD=（8-x）cm，在Rt△ACD中利用勾股定理得到x2+62=（8-x）2，然后解方程即可．
解答 解：∵△ABC折叠，使点B与点A重合，折痕为DE，
∴DA=DB，
设CD=xcm，则BD=AD=（8-x）cm，
在Rt△ACD中，∵CD2+AC2=AD2，
∴x2+62=（8-x）2，解得x=$\frac{7}{4}$，
即CD的长为$\frac{7}{4}$．
故选C．
点评 本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了勾股定理．
练习册系列答案
相关题目
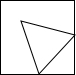
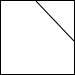
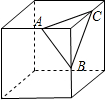如图，是一个切去了一个角的正方体，切面与棱的交点A，B，C均是棱的中点，得到的几何体的主视图是（ ）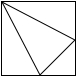
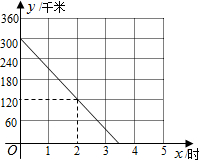A、B两座城市之间有一条高速公路，甲、乙两辆汽车同时分别从这条路两端的入口处驶入，并始终在高速公路上正常行驶．甲车驶往B城，乙车驶往A城，甲车在行驶过程中速度始终不变．甲车距B城高速公路入口处的距离y（千米）与行驶时间x（时）之间的关系如图．
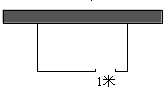如图是长方形鸡场平面示意图，一边靠墙（墙足够长），另外三边用竹篱笆围成，在其中一边上有一个1米长的小门（用其它材料制成），若竹篱笆总长为34米，所围的面积为150平方米，求此长方形鸡场的长、宽分别为多少米？
13．下列二次根式属于最简二次根式的是（ ）
| A． | $\sqrt{8}$ | B． | $\sqrt{3}$ | C． | $\sqrt{\frac{2}{5}}$ | D． | $\sqrt{1.4}$ |