题目内容
已知直线y=| 1 | 2 |
(1)求b的值;
(2)把△AOB绕原点O顺时针旋转90°后,点A落在y轴的A′处,点B若在x轴的B′处.
①求直线A′B′的函数关系式;
②设直线AB与直线A′B′交于点C,矩形PQMN是△AB′C的内接矩形,其中点P,Q在线段AB′上,点M在线段B′C上,点N在线段AC上.若矩形PQMN的两条邻边的比为1:2,试求矩形PQMN的周长.
分析:(1)点A在直线上,直接代入即可得b;
(2)①根据旋转性质确定旋转后A′B′坐标,即可得解析式;
②根据几何图形,确定P、Q、M、N四点的关系即可确定周长.
(2)①根据旋转性质确定旋转后A′B′坐标,即可得解析式;
②根据几何图形,确定P、Q、M、N四点的关系即可确定周长.
解答: 解:(1)由题意得
解:(1)由题意得
把A(-4,0)代入y=
x+b,
得
×(-4)+b=0,b=2;(3分)
(2)①由(1)得:y=
x+2,
令x=0,得y=2,
∴B(0,2)(4分)
由旋转性质可知OA'=OA=4,OB'=OB=2
∴A'(0,4),B'(2,0)(5分)
设直线A'B'的解析式为y=ax+b,
把A'、B'分别代入得:
,解得
∴直线A'B'的解析式为y=-2x+4;(7分)
②∵点N在AC上
∴可设N(x,
x+2)(-4<x<0)
∵四边形PQMN为矩形
∴NP=MQ=
x+2(8分)
(ⅰ)当PN:PQ=1:2时
PQ=2PN=2(
x+2)=x+4
∴Q(x+4+x,0)
∴M(2x+4,
x+2)
∵点M在B'C上
∴-2(2x+4)+4=
x+2
解得x=-
此时,PQ=
∴矩形PQMN的周长为2(
+
)=8(10分)
(ⅱ)当PN:PQ=2:1时
PQ=
PN=
(
x+2)=
x+1
∴Q(
x+1+x,0)
M(
x+1,
x+2)
∵点M在B'C上
∴-2(
x+1)+4=
x+2
解得x=0
此时PN=2,PQ=1
∴矩形PQMN的周长为2(2+1)=6.(12分)
综上所述,当PN:PQ=1:2时,矩形PQMN的周长为8.
当PQ:PN=1:2时,矩形PQMN的周长为6.(13分)
 解:(1)由题意得
解:(1)由题意得把A(-4,0)代入y=
| 1 |
| 2 |
得
| 1 |
| 2 |
(2)①由(1)得:y=
| 1 |
| 2 |
令x=0,得y=2,
∴B(0,2)(4分)
由旋转性质可知OA'=OA=4,OB'=OB=2
∴A'(0,4),B'(2,0)(5分)
设直线A'B'的解析式为y=ax+b,
把A'、B'分别代入得:
|
|
∴直线A'B'的解析式为y=-2x+4;(7分)
②∵点N在AC上
∴可设N(x,
| 1 |
| 2 |
∵四边形PQMN为矩形
∴NP=MQ=
| 1 |
| 2 |
(ⅰ)当PN:PQ=1:2时
PQ=2PN=2(
| 1 |
| 2 |
∴Q(x+4+x,0)
∴M(2x+4,
| 1 |
| 2 |
∵点M在B'C上
∴-2(2x+4)+4=
| 1 |
| 2 |
解得x=-
| 4 |
| 3 |
此时,PQ=
| 8 |
| 3 |
∴矩形PQMN的周长为2(
| 4 |
| 3 |
| 8 |
| 3 |
(ⅱ)当PN:PQ=2:1时
PQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∴Q(
| 1 |
| 4 |
M(
| 5 |
| 4 |
| 1 |
| 2 |
∵点M在B'C上
∴-2(
| 5 |
| 4 |
| 1 |
| 2 |
解得x=0
此时PN=2,PQ=1
∴矩形PQMN的周长为2(2+1)=6.(12分)
综上所述,当PN:PQ=1:2时,矩形PQMN的周长为8.
当PQ:PN=1:2时,矩形PQMN的周长为6.(13分)
点评:本题考查待定系数法求一次函数及其坐标特征,并综合几何旋转性质应用,是个综合性比较高的题,要求要熟练掌握函数图象性质.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 已知直线
已知直线 E两点,与x轴交于B、C两点,且B点坐标为(1,0).
E两点,与x轴交于B、C两点,且B点坐标为(1,0).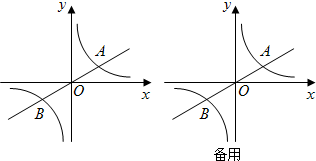
 (2013•梧州模拟)如图,已知直线y=
(2013•梧州模拟)如图,已知直线y=