题目内容
如图,在直角三角形ABC中,∠ABC=90°.
(1)先作∠ACB的平分线;设它交AB边于点O,再以点O为圆心,OB为半径作⊙O(尺规作图,保留作图痕迹,不写作法);
(2)证明:AC是所作⊙O的切线;
(3)若BC=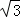 ,sinA=
,sinA=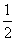 ,求△AOC的面积.
,求△AOC的面积.
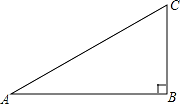
(1)解:如图所示:
(2)证明:过点O作OE⊥AC于点E,
∵FC平分∠ACB,
∴OB =OE,OB=r ,OE=d
=OE,OB=r ,OE=d
∴r=d
∴AC是所作⊙O的切线;
(3)解:∵sinA=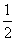 ,∠ABC=90°,
,∠ABC=90°,
∴∠A=30°,
∴∠ACB=∠OCB=ACB=30°,
∵BC=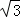 ,
,
∴AC=2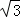 ,BO=tan30°BC=
,BO=tan30°BC= ×
× =1,
=1,
∴△AOC的面积为: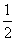 ×AC×OE=
×AC×OE=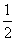 ×2
×2 ×1=
×1= .
.

练习册系列答案
相关题目
 车由A地驶向C站、货车由B地驶向A地,两车同时出发,匀速行驶,货车的速度是客车速度的
车由A地驶向C站、货车由B地驶向A地,两车同时出发,匀速行驶,货车的速度是客车速度的  . 图2 是客、货车离C站的路程y1、y2(千米)与行驶时间x(小时)之间的函数关系图象.
. 图2 是客、货车离C站的路程y1、y2(千米)与行驶时间x(小时)之间的函数关系图象. 关系式;
关系式; 求E点坐标,并说明点E的实际意义.
求E点坐标,并说明点E的实际意义.

 的不等式组
的不等式组 只有四个整数解,则实数
只有四个整数解,则实数 的取值范围是
的取值范围是

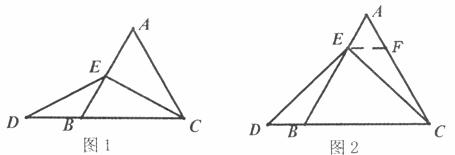
 AC于点F.(请你补充完成解答过程)
AC于点F.(请你补充完成解答过程)