题目内容
5.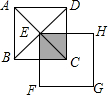 如图,边长均为2的正方形ABCD与正方形EFGH相互重合,点E在AC与BD的交点处,若将正方形EFGH绕点E顺时针旋转,设两正方形重合的面积(阴影部分)为S,旋转的角度为α,则能大致反映S与α之间函数关系的图象是( )
如图,边长均为2的正方形ABCD与正方形EFGH相互重合,点E在AC与BD的交点处,若将正方形EFGH绕点E顺时针旋转,设两正方形重合的面积(阴影部分)为S,旋转的角度为α,则能大致反映S与α之间函数关系的图象是( )| A. | 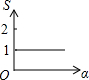 | B. | 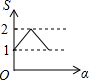 | C. | 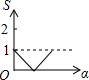 | D. | 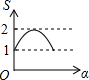 |
分析 过点E作EM⊥CD于点M,EN⊥AD于点N,则可证明△ENK≌△EML,从而得出重叠部分的面积不变,继而可得出函数关系图象.
解答 解:如图,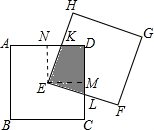
过点E作EM⊥CD于点M,EN⊥AD于解:如右图,过点E作EM⊥CD于点M,EN⊥AD于点N,
∵点E是正方形的对称中心,
∴EN=EM,
由旋转的性质可得∠NEK=∠MEL,
在Rt△ENK和Rt△EML中,
$\left\{\begin{array}{l}{∠NEK=∠MEL}\\{EN=EM}\\{∠ENK=∠EML}\end{array}\right.$,
故可得△ENK≌△EML,即阴影部分的面积始终等于正方形面积的$\frac{1}{4}$.
故选:A.
点评 此题考查了动点问题的函数图象,证明△ENK≌△EML,得出阴影部分的面积始终等于正方形面积的$\frac{1}{4}$是解答本题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
15.在△ABC中,∠C=90°,AB的垂直平分线DE交AB于E,交BC于D,且CD:BD=1:2,BC=6cm,则D到AB的距离为多少( )
| A. | 1.5cm | B. | 2cm | C. | 3cm | D. | 4cm |
16.用配方法解方程x2+4x-5=0,下列配方正确的是( )
| A. | (x+2)2=1 | B. | (x+2)2=5 | C. | (x+2)2=9 | D. | (x+4)2=9 |
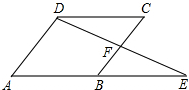 已知:如图,在?ABCD中,延长AB到点E,使BE=AB,连接DE交BC于点F.求证:△BEF≌△CDF.
已知:如图,在?ABCD中,延长AB到点E,使BE=AB,连接DE交BC于点F.求证:△BEF≌△CDF.