Question

【题目】问题探究

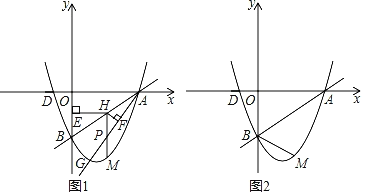
（1）如图1，△ABC和△DEC均为等腰直角三角形，∠ACB＝∠DCE＝90°，点B，D，E在同一直线上，连接AD，BD．

①请探究AD与BD之间的位置关系：________；

②若AC＝BC＝，DC＝CE＝，则线段AD的长为________；

拓展延伸

（2）如图2，△ABC和△DEC均为直角三角形，∠ACB＝∠DCE＝90°，AC＝，BC＝，CD＝，CE＝1．将△DCE绕点C在平面内顺时针旋转，设旋转角∠BCD为α（0°≤α＜360°），作直线BD，连接AD，当点B，D，E在同一直线上时，画出图形，并求线段AD的长．

Answer 1

【答案】（1）①垂直，②4；（2）作图见解析，或

【解析】

（1）①由“SAS”可证△ACD≌△BCE，可得∠ADC=∠BEC=45°，可得AD⊥BD；

②过点C作CF⊥AD于点F，由勾股定理可求DF，CF，AF的长，即可求AD的长；

（2）分点D在BC左侧和BC右侧两种情况讨论，根据勾股定理和相似三角形的性质可求解．

解：（1）∵△ABC和△DEC均为等腰直角三角形，

∴AC=BC，CE=CD，∠ABC=∠DEC=45°=∠CDE

∵∠ACB=∠DCE=90°，

∴∠ACD=∠BCE，且AC=BC，CE=CD

∴△ACD≌△BCE（SAS）

∴∠ADC=∠BEC=45°

∴∠ADE=∠ADC+∠CDE=90°

∴AD⊥BD

故答案为：垂直

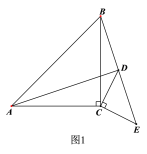
②如图，过点C作CF⊥AD于点F，

∵∠ADC=45°，CF⊥AD，CD=

∴DF=CF=1

∴

∴AD=AF+DF=4

故答案为：4．

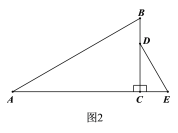
（2）①如图：

∵∠ACB＝∠DCE＝90°，AC＝，BC＝，CD＝，CE＝1，

∴AB=2,DE=2,∠ACD＝∠BCE, ．

∴△ACD∽△BCE．

∴∠ADC＝∠E，．

又∵∠CDE+∠E=90°，

∴∠ADC+∠CDE =90°，即∠ADE=90°．

∴AD⊥BE．

设BE=x，则AD=x．

在Rt△ABD中，，

即．

解得（负值舍去）．

∴AD=．

②如图，

同①设BE=x，则AD=x．

在Rt△ABD中，，即．

解得（负值舍去）．

∴AD=．

综上可得，线段AD的长为