题目内容
在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线.
(1)如图,若点B、C在AE的异侧,BD⊥AE于点D,CE⊥AE于点E.求证:BD=DE+CE;

(2)若直线AE绕点A旋转到下图的位置时(BD<CE),其余条件不变,问BD与DE、CE的关于如何?并证明你的结论.

答案:
解析:
解析:
|
解:(1)证明:因为BD⊥AE,CE⊥AE, 所以∠BDA=∠AEC=90°. 因为∠BAD+∠CAE=90°,∠BAD+∠ABD=90°, 所以∠CAE=∠ABD. 在△ABD和△CAE中, 因为 所以△ABD≌△CAE.所以BD=AE,AD=CE. 因为AE=AD+DE,所以BD=CE+DE. (2)BD=DE-CE,证明方法与(1)相似. |

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目

 ;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.
;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.
 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.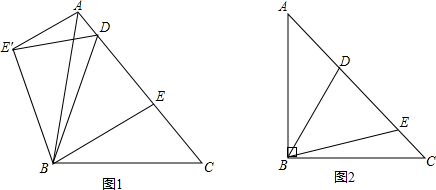
 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以每秒4cm,的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以每秒4cm,的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.