题目内容
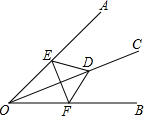 如图,已知射线OC上的任意一点到∠AOB的两边的距离都相等,点D、E、F分别为边OC、OA、OB上,如果要想证得OE=OF,只需要添加以下四个条件中的某一个即可,请写出所有可能的条件的序号
如图,已知射线OC上的任意一点到∠AOB的两边的距离都相等,点D、E、F分别为边OC、OA、OB上,如果要想证得OE=OF,只需要添加以下四个条件中的某一个即可,请写出所有可能的条件的序号①∠ODE=∠ODF;②∠OED=∠OFD;③ED=FD;④EF⊥OC.
考点:角平分线的性质,全等三角形的判定与性质
专题:
分析:由射线OC上的任意一点到∠AOB的两边的距离都相等,根据角平分线的判定定理可知OC平分∠AOB.要得到OE=OF,就要让△ODE≌△ODF,①②④都行,只有③ED=FD不行,因为证明三角形全等没有边边角定理.
解答: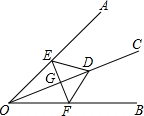 解:∵射线OC上的任意一点到∠AOB的两边的距离都相等,
解:∵射线OC上的任意一点到∠AOB的两边的距离都相等,
∴OC平分∠AOB.
①若①∠ODE=∠ODF,根据ASA定理可求出△ODE≌△ODF,由三角形全等的性质可知OE=OF.正确;
②若∠OED=∠OFD,根据AAS定理可得△ODE≌△ODF,由三角形全等的性质可知OE=OF.正确;
③若ED=FD条件不能得出.错误;
④若EF⊥OC,根据ASA定理可求出△OGE≌△OGF,由三角形全等的性质可知OE=OF.正确.
故答案为①②④.
 解:∵射线OC上的任意一点到∠AOB的两边的距离都相等,
解:∵射线OC上的任意一点到∠AOB的两边的距离都相等,∴OC平分∠AOB.
①若①∠ODE=∠ODF,根据ASA定理可求出△ODE≌△ODF,由三角形全等的性质可知OE=OF.正确;
②若∠OED=∠OFD,根据AAS定理可得△ODE≌△ODF,由三角形全等的性质可知OE=OF.正确;
③若ED=FD条件不能得出.错误;
④若EF⊥OC,根据ASA定理可求出△OGE≌△OGF,由三角形全等的性质可知OE=OF.正确.
故答案为①②④.
点评:本题主要考查了角平分线的判定,三角形全等的判定与性质;由求线段相等转化为添加条件使三角形全等是正确解答本题的关键.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
下列每组数分别表示三根木棒的长度,将它们首位连接后,能摆成三角形的一组是( )
| A、1,2,4 |
| B、2,2,4 |
| C、1,2,3 |
| D、2,3,4 |
 已知:如图,在△ABC中,AB=AC,∠C=30°,AD⊥AB,AD=4cm,求DC、BC、AC的长.
已知:如图,在△ABC中,AB=AC,∠C=30°,AD⊥AB,AD=4cm,求DC、BC、AC的长.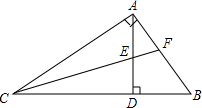 如图,在△ABC中,∠BAC=90°,AD⊥BC于D,∠ACB的平分线交AD于E,交AB于F,请猜测∠AEF与∠AFE之间有怎样的数量关系,并说明理由.
如图,在△ABC中,∠BAC=90°,AD⊥BC于D,∠ACB的平分线交AD于E,交AB于F,请猜测∠AEF与∠AFE之间有怎样的数量关系,并说明理由.