题目内容
在直角坐标系xOy中，点P（4，y）在第四象限内，且OP与x轴正半轴的夹角的正切值是2，则y的值是
- A.2
- B.8
- C.-2
- D.-8
D
分析：如图，由于点P（4，y）在第四象限内，所以OA=4，又OP与x轴正半轴的夹角的正切值是2，所以tan∠AOP=2，然后利用三角函数的定义即可求解．
解答：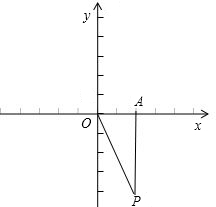
解：如图，
∵点P（4，y）在第四象限内，
∴OA=4，PA=-y
又OP与x轴正半轴的夹角的正切值是2，
∴tan∠AOP=2，
∴
=2，
∴-y=2×4，
∴y=-8．
故选D．
点评：此题主要考查了三角函数的定义，也考查了数形结合的思想，解题时首先利用数形结合的思想利用坐标表示线段的长度，然后利用三角函数的定义列出方程即可解决问题．
分析：如图，由于点P（4，y）在第四象限内，所以OA=4，又OP与x轴正半轴的夹角的正切值是2，所以tan∠AOP=2，然后利用三角函数的定义即可求解．
解答：
解：如图，∵点P（4，y）在第四象限内，
∴OA=4，PA=-y
又OP与x轴正半轴的夹角的正切值是2，
∴tan∠AOP=2，
∴
=2，∴-y=2×4，
∴y=-8．
故选D．
点评：此题主要考查了三角函数的定义，也考查了数形结合的思想，解题时首先利用数形结合的思想利用坐标表示线段的长度，然后利用三角函数的定义列出方程即可解决问题．
练习册系列答案
相关题目
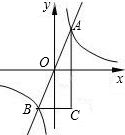在直角坐标系xoy中，函数y=4x的图象与反比例函数y=
（2012•北京二模）已知：如图，在直角坐标系xOy中，点A（8，0）、B（0，6），点C在x轴的负半轴上，AB=AC．动点M在x轴上从点C向点A移动，动点N在线段AB上从点A向点B移动，点M、N同时出发，且移动的速度都为每秒1个单位，移动时间为t秒（0＜t＜10）．
析式为y=x2-mx+n．方程x2-mx+n=0的两根倒数和为-4．