题目内容
观察下列等式:1×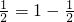 ,2×
,2×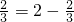 ,3×
,3×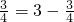 ,…那么根据以上规律可知第n(n为整数)等式为________.
,…那么根据以上规律可知第n(n为整数)等式为________.
n× =n-
=n- (n为正整数)
(n为正整数)
分析:通过观察1× =1-
=1- ,2×
,2× =2-
=2- ,3×
,3× =3-
=3- ,可以得到这些等式都是两个数的积等于这两个数的差,而这两个数中一个数为正整数,另一个数为分数(其分子等于前面的正整数,分母比分子大1),则第n(n为正整数)等式为为n×
,可以得到这些等式都是两个数的积等于这两个数的差,而这两个数中一个数为正整数,另一个数为分数(其分子等于前面的正整数,分母比分子大1),则第n(n为正整数)等式为为n× =n-
=n- (n为正整数).
(n为正整数).
解答:∵1× =1-
=1- ,
,
2× =2-
=2- ,
,
3× =3-
=3- ,
,
…,
所以n× =n-
=n- (n为正整数).
(n为正整数).
故答案为n× =n-
=n- (n为正整数).
(n为正整数).
点评:本题考查了规律型:数字的变化类:通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.
 =n-
=n- (n为正整数)
(n为正整数)分析:通过观察1×
 =1-
=1- ,2×
,2× =2-
=2- ,3×
,3× =3-
=3- ,可以得到这些等式都是两个数的积等于这两个数的差,而这两个数中一个数为正整数,另一个数为分数(其分子等于前面的正整数,分母比分子大1),则第n(n为正整数)等式为为n×
,可以得到这些等式都是两个数的积等于这两个数的差,而这两个数中一个数为正整数,另一个数为分数(其分子等于前面的正整数,分母比分子大1),则第n(n为正整数)等式为为n× =n-
=n- (n为正整数).
(n为正整数).解答:∵1×
 =1-
=1- ,
,2×
 =2-
=2- ,
,3×
 =3-
=3- ,
,…,
所以n×
 =n-
=n- (n为正整数).
(n为正整数).故答案为n×
 =n-
=n- (n为正整数).
(n为正整数).点评:本题考查了规律型:数字的变化类:通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目