题目内容

如图，CD是Rt△ABC斜边AB边上的高，AB=10cm，BC=8cm，则sin∠ACD=（　　）
A、
3
4
B、
3
5
C、
4
5
D、
4
3
考点：锐角三角函数的定义,勾股定理
专题：
分析：利用勾股定理求得AC的长，然后证明∠ACD=∠B，则sin∠ACD=sin∠B=
AC
AB
，从而求解．
解答：解：在直角△ABC中，AC=
AB2-BC2
=
102-82
=6，
∵在△ACD和△ABC中，∠A=∠A，∠ADC=∠ACB=90°，
∴∠ACD=∠B，
∴sin∠ACD=sin∠B=
AC
AB
=
6
10
=
3
5
．
点评：本题考查了勾股定理以及三角函数，关键是理解三角函数的值是由角的大小确定的．
练习册系列答案
相关题目
已知点P（-3，4），则点P到x轴的距离是（　　）
A、-3B、-4C、3D、4
在弹性限度内，弹簧深长的长度与拉力成正比．如图小明手中拿着由三根相同的弹簧组成的弹簧拉力器．已知拉力器的长度y与拉力x是一次函数关系，y与x的部分对应值如下表．
x（单位：N） 0 120 420
y（单位：cm） 28 30 35
（1）求y与x之间的函数关系，并直接写出y的取值范围．
（2）已知小明的最大拉力为100N．求小明能使单根弹簧伸长的最大长度．
直角坐标平面内，点O（0，0）、点A（3，3）、点B（3，-2），则△ABC的面积是
 
．
如果点P（a，2）在第二象限，那么点Q（-3，a）关于y轴的对称点再向下平移7各单位后在第
 
象限．
去年某市有1530人参加中考，为了了解他们的数学成绩，从中抽取200名考生的数学成绩，其中有62名考生达到优秀，那么该市约有多少名考生达到优秀（　　）
A、500名B、475名
C、450名D、400名
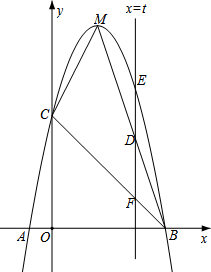如图，抛物线y=ax2+bx+c（a≠0）与x轴交于A、B两点，其中A点坐标为（-1，0），线段AB=6，sin∠ABC=
2
2
，M为抛物线的顶点．
（1）求抛物线的解析式；
（2）求△MCB的面积；
（3）若点D为线段BM上任一点（点D不与点B重合，可与点M重合），过点D作垂直于x轴的直线x=t，交抛物线于点E，交线段BC于点F．
①求当t为何值时，线段DE有最大值？最大值是多少？
②是否存在这样的点D，使得
ED
FD
=
1
2
？若存在，求出D点的坐标；若不存在，则请说明理由．
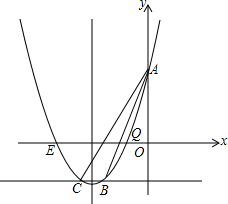如图，已知抛物线y=ax2+bx+c与y轴交于A（0，4），且抛物线经过点C（-3，-2），对称轴x=-
5
2
．
（1）求出抛物线的解析式；
（2）过点C作x轴的平行线交抛物线于B点，连接AC，AB，若在抛物线上有一点D，使得
3
2
△ABC=S△BCD，求D点的坐标；
（3）记抛物线与x轴左交点为E，在A、E两点之间的抛物线上有一点F，连接AE、FE、FA，试求出使得S△AEF面积最大时，F点的坐标以及此时的面积．
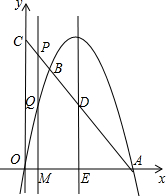如图，点A是抛物线y=-
5
8
x2+5x与x轴正半轴的交点，点B在这条抛物线上，且点B的横坐标为2．连接AB并延长交y轴于点C，抛物线的对称轴交AC于点D，交x轴于点E．点P在线段CA上，过点P作x轴的垂线，垂足为点M，交抛物线于点Q．设点P的横坐标为m．
（1）求直线AB对应的函数解析式．
（2）当四边形DEMQ为矩形时，求点Q的坐标．
（3）设线段PQ的长为d（d＞0），求d关于m的函数解析式．
（4）在（3）的情况下，请直接写出当d随着m的增大而减小时，m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网