题目内容
求值:
(1)若a= +1,b=
+1,b= -1,求a2b+ab2的值;
-1,求a2b+ab2的值;
(2)若x+y=-5,xy=3,求 的值.
的值.
解:(1)∵a= +1,b=
+1,b= -1,
-1,
∴a+b=2 ,ab=(
,ab=( )2-1=2,
)2-1=2,
∴a2b+ab2=ab(a+b)=2×2 =4
=4 ;
;
(2)∵x+y=-5,xy=3,
∴x<0,y<0,
∴ +
+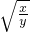 =
= +
+
= +
+
=- -
-
=- •
•
=- ×
×
= .
.
分析:(1)由于a= +1,b=
+1,b= -1,可计算得到a+b=2
-1,可计算得到a+b=2 ,ab=(
,ab=( )2-1=2,然后变形a2b+ab2=ab(a+b),再利用整体思想进行计算;
)2-1=2,然后变形a2b+ab2=ab(a+b),再利用整体思想进行计算;
(2)由于x+y=-5,xy=3得到x<0,y<0,利用二次根式的性质化简 +
+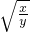 =
= +
+ =
= +
+ =-
=- -
- =-
=- •
• ,再利用整体思想进行计算.
,再利用整体思想进行计算.
点评:本题考查了二次根式的化简求值:先根据已知条件得到两个字母的和与积的值,然后变形所求的代数式,用这两个字母的和与积来表示,再运用整体代入的方法求代数式的值.
 +1,b=
+1,b= -1,
-1,∴a+b=2
 ,ab=(
,ab=( )2-1=2,
)2-1=2,∴a2b+ab2=ab(a+b)=2×2
 =4
=4 ;
;(2)∵x+y=-5,xy=3,
∴x<0,y<0,
∴
 +
+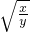 =
= +
+
=
 +
+
=-
 -
-
=-
 •
•
=-
 ×
×
=
 .
.分析:(1)由于a=
 +1,b=
+1,b= -1,可计算得到a+b=2
-1,可计算得到a+b=2 ,ab=(
,ab=( )2-1=2,然后变形a2b+ab2=ab(a+b),再利用整体思想进行计算;
)2-1=2,然后变形a2b+ab2=ab(a+b),再利用整体思想进行计算;(2)由于x+y=-5,xy=3得到x<0,y<0,利用二次根式的性质化简
 +
+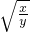 =
= +
+ =
= +
+ =-
=- -
- =-
=- •
• ,再利用整体思想进行计算.
,再利用整体思想进行计算.点评:本题考查了二次根式的化简求值:先根据已知条件得到两个字母的和与积的值,然后变形所求的代数式,用这两个字母的和与积来表示,再运用整体代入的方法求代数式的值.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目