题目内容
如图,直线 与
与 轴相交于点
轴相交于点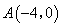 ,与
,与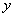 轴相交于点
轴相交于点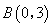 ,点
,点 从点
从点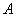 出发,以每秒
出发,以每秒 个单位长度的速度沿直线
个单位长度的速度沿直线 向点
向点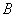 移动。同时,将直线
移动。同时,将直线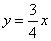 以每秒
以每秒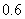 个单位长度的速度向上平移,交
个单位长度的速度向上平移,交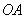 于点
于点 ,交
,交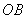 于点
于点 ,设运动时间为
,设运动时间为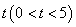 秒。
秒。
⑴证明:在运动过程中,四边形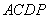 总是平行四边形;
总是平行四边形;
⑵当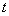 取何值时,四边形
取何值时,四边形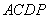 为菱形?请指出此时以点
为菱形?请指出此时以点 为圆心、
为圆心、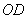 长为半径的圆与直线
长为半径的圆与直线 的位置关系并说明理由。
的位置关系并说明理由。
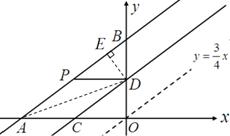
解:⑴∵直线 与
与 轴相交于点
轴相交于点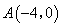 ,与
,与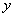 轴相交于点
轴相交于点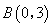
∴直线 的解析式为
的解析式为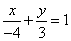 ,即
,即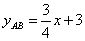
∵将直线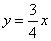 以每秒
以每秒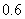 个单位长度的速度向上平移
个单位长度的速度向上平移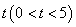 秒得到直线
秒得到直线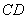
∴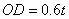 ,∴
,∴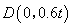 ,∴直线
,∴直线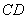 的解析式为
的解析式为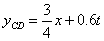
∵在直线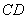 中,点
中,点 在
在 轴上,∴令
轴上,∴令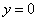 ,则
,则 ,∴
,∴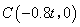 ,
,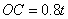
∴在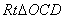 中,
中,
∵点 从点
从点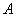 出发,以每秒
出发,以每秒 个单位长度的速度沿直线
个单位长度的速度沿直线 向点
向点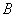 移动
移动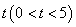 秒
秒
∴ ,∴
,∴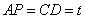 ,又∵
,又∵ ,∴
,∴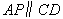 ,
,
∵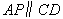 ,
,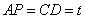 ,∴在运动过程中,四边形
,∴在运动过程中,四边形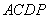 总是平行四边形;
总是平行四边形;
⑵欲使四边形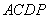 为菱形,只需在
为菱形,只需在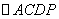 中满足条件
中满足条件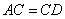 ,即
,即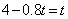 ,解得
,解得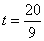
∴当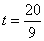 时,四边形
时,四边形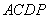 为菱形;
为菱形;
此时以点 为圆心、
为圆心、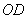 长为半径的圆与直线
长为半径的圆与直线 相切,理由如下:
相切,理由如下:
∵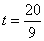 ,∴
,∴ ,∴
,∴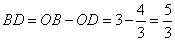
∵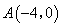 ,
,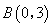 ,∴
,∴ ,
,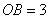 ,∴在
,∴在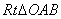 中,
中,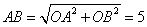
过点 作
作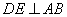 于点
于点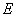 ,则
,则
∵在 和
和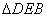 中,
中,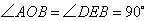 且
且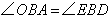 ,∴
,∴ ∽
∽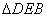
∴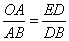 ,即
,即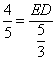 ,∴
,∴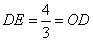 ,∴点
,∴点 到直线
到直线 的距离等于
的距离等于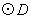 的半径
的半径
∴以点 为圆心、
为圆心、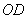 长为半径的圆与直线
长为半径的圆与直线 相切。
相切。
另解:(在证明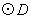 与直线
与直线 相切时,也可利用等积法求得点
相切时,也可利用等积法求得点 到直线
到直线 的距离。)
的距离。)
设点 到直线
到直线 的距离为
的距离为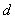 ,则
,则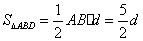 ,连结
,连结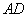 ,
,
∵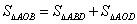 且
且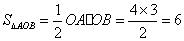 、
、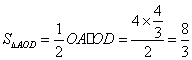
∴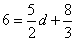 ,解得
,解得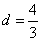 ,∴点
,∴点 到直线
到直线 的距离与
的距离与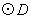 的半径相等,即
的半径相等,即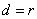
∴以点 为圆心、
为圆心、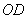 长为半径的
长为半径的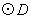 与直线
与直线 相切。
相切。
再解:(巧用“菱形对角线的性质”和“角平分线性质定理”)
连结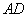 ,则
,则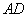 是菱形
是菱形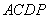 的对角线,∴
的对角线,∴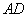 平分
平分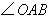
∵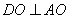 ,∴
,∴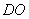 是点
是点 到直线
到直线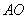 的距离,
的距离,
∴点 到直线
到直线 的距离=点
的距离=点 到直线
到直线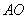 的距离
的距离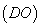
∴以点 为圆心、
为圆心、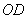 长为半径的圆与直线
长为半径的圆与直线 相切。
相切。

练习册系列答案
相关题目
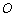 ,引一条有方向的射线
,引一条有方向的射线 ,再选定一个单位长度,那么平面上任一点M的位置可由
,再选定一个单位长度,那么平面上任一点M的位置可由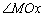 的度数
的度数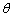 与
与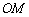 的长度m确定,有序数对(
的长度m确定,有序数对(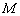 点的“极坐标”,这样建立的坐标系称为“极坐标系”.
点的“极坐标”,这样建立的坐标系称为“极坐标系”.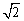 ) D.(50°,2
) D.(50°,2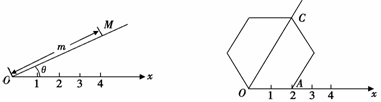
 图4
图4 中,
中, ,
, ,则
,则 的长为。
的长为。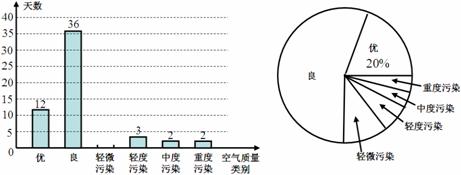
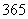 天)达到“优”和“良”的总天数。
天)达到“优”和“良”的总天数。
 中自变量
中自变量 是取值范围是 .
是取值范围是 .