题目内容
如图，锐角三角形ABC内接于⊙O，已知∠B=48°，则∠OAC=________．
42°
分析：连接OA，由圆周角定理可求出∠AOC的度数，再根据OA=OC可知∠OAC=∠OCA，再由三角形内角和定理即可求出答案．
解答：
解：连接OA，
∵∠ABC=48°，
∴∠AOC=96°，
∵OA=OC，
∴∠OAC=∠OCA=
=
=42°．
故答案为：42°．
点评：本题考查的是圆周角定理、三角形内角和定理及等腰三角形的性质，根据题意作出辅助线，构造出等腰三角形是解答此题的关键．
分析：连接OA，由圆周角定理可求出∠AOC的度数，再根据OA=OC可知∠OAC=∠OCA，再由三角形内角和定理即可求出答案．
解答：
解：连接OA，∵∠ABC=48°，
∴∠AOC=96°，
∵OA=OC，
∴∠OAC=∠OCA=
==42°．故答案为：42°．
点评：本题考查的是圆周角定理、三角形内角和定理及等腰三角形的性质，根据题意作出辅助线，构造出等腰三角形是解答此题的关键．
练习册系列答案
相关题目
16、如图，锐角三角形ABC的边AB，AC上的高线CE和BF相交于点D，请写出图中的两对相似三角形：
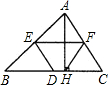如图，锐角三角形ABC中（AB＞AC），AH⊥BC，垂足为H，E、D、F分别是各边的中点，则四边形EDHF是（ ）| A、梯形 | B、等腰梯形 | C、直角梯形 | D、矩形 |
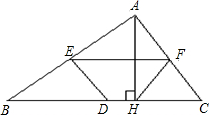如图，锐角三角形ABC中，（AB＞AC），AH⊥BC，垂足为H，E、D、F分别是各边的中点，求证：四边形EDHF是等腰梯形．
28、如图，锐角三角形ABC中，BC＞AB＞AC，小靖依下列方法作图：
如图，锐角三角形ABC中，AD⊥BC，BE⊥AC，垂足分别为D和E，AP∥BC且与BE的延长线交于点P，又边AB、AC的长是关于x的一元二次方程x2-x+