题目内容
如图,在梯形ABCD中,AB∥DC,AB=2,DC=10,AD=BC=5,点M、N分别在AD、BC上运动,并保持M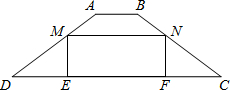 N∥AB,ME⊥DC,NF⊥DC,垂足分别为E、F.
N∥AB,ME⊥DC,NF⊥DC,垂足分别为E、F.
(1)求梯形ABCD的面积;
(2)探究一:四边形MNFE的面积有无最大值?若有,请求出这个最大值;若无,请说明理由;
(3)探究二:四边形MNFE能否为正方形?若能,请求出正方形的面积;若不能,请说明理由.
解:(1)如图,
过点A作AG⊥CD于G,过B作BQ⊥DC于Q,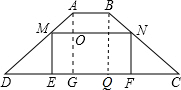
则AG∥BQ,
∵AB∥DC,
∴四边形AGQB是平行四边形,
∴AB=GQ=2,AG=BQ,
由勾股定理得:DG=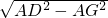 ,CQ=
,CQ=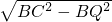 ,
,
∵AD=BC,AG=BQ,
∴DG=CQ=(10-2)÷2=4,
在Rt△ADG中,AG=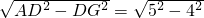 =3,
=3,
∴S梯形ABCD=(2+10)×3÷2=18;
(2)设MN=x,AG与MN交于点O,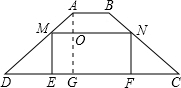
∵MN∥CD,
∴△AMO∽△ADG,
∴MO:DG=AO:AG,
即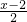 :
: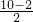 =AO:3,
=AO:3,
∴AO=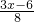 ,
,
∴OG=3-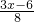 =
=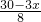 ,
,
∴S矩形MNFE=x•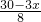 =
= x-
x- x2,
x2,
∵二次项系数小于0,
∴当x=5时,四边形MNFE的面积有最大值:[4×(- )×0-(
)×0-( )2]÷[4×(-
)2]÷[4×(- )]=
)]=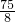 ;
;
(3)当MN=ME时,四边形MNFE能为正方形.
由(2)可得,ME=OG=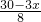 ,
,
则=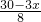 =x,
=x,
解得x=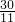 ,
,
此时,正方形MNFE的面积为:(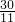 )2=
)2=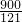 .
.
分析:(1)要求梯形ABCD的面积,需先求梯形的高,可作高根据勾股定理易求得;
(2)尝试把四边形MNFE的面积用二次函数的形式表达出来,再由二次函数的最值问题讨论;
(3)在(2)的基础上,使MN=ME,求解即可.
点评:此题考查了梯形的面积、二次函数的最值、正方形的判定等知识点,综合性很强.
过点A作AG⊥CD于G,过B作BQ⊥DC于Q,

则AG∥BQ,
∵AB∥DC,
∴四边形AGQB是平行四边形,
∴AB=GQ=2,AG=BQ,
由勾股定理得:DG=
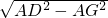 ,CQ=
,CQ=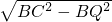 ,
,∵AD=BC,AG=BQ,
∴DG=CQ=(10-2)÷2=4,
在Rt△ADG中,AG=
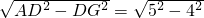 =3,
=3,∴S梯形ABCD=(2+10)×3÷2=18;
(2)设MN=x,AG与MN交于点O,

∵MN∥CD,
∴△AMO∽△ADG,
∴MO:DG=AO:AG,
即
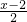 :
: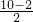 =AO:3,
=AO:3,∴AO=
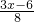 ,
,∴OG=3-
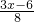 =
=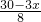 ,
,∴S矩形MNFE=x•
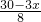 =
= x-
x- x2,
x2,∵二次项系数小于0,
∴当x=5时,四边形MNFE的面积有最大值:[4×(-
 )×0-(
)×0-( )2]÷[4×(-
)2]÷[4×(- )]=
)]=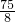 ;
;(3)当MN=ME时,四边形MNFE能为正方形.
由(2)可得,ME=OG=
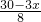 ,
,则=
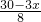 =x,
=x,解得x=
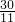 ,
,此时,正方形MNFE的面积为:(
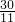 )2=
)2=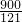 .
.分析:(1)要求梯形ABCD的面积,需先求梯形的高,可作高根据勾股定理易求得;
(2)尝试把四边形MNFE的面积用二次函数的形式表达出来,再由二次函数的最值问题讨论;
(3)在(2)的基础上,使MN=ME,求解即可.
点评:此题考查了梯形的面积、二次函数的最值、正方形的判定等知识点,综合性很强.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )
如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )| A、3cm | B、7cm | C、3cm或7cm | D、2cm |
 11、如图,在梯形ABCD中,AB∥CD,对角线AC、BD交于点O,则S△AOD
11、如图,在梯形ABCD中,AB∥CD,对角线AC、BD交于点O,则S△AOD 已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=CD=10.
已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=CD=10. 如图,在梯形ABCD中,AD∥BC,AB⊥AD,对角线BD⊥DC.
如图,在梯形ABCD中,AD∥BC,AB⊥AD,对角线BD⊥DC. 20、如图,在梯形ABCD中,AD∥BC,并且AB=8,AD=3,CD=6,并且∠B+∠C=90°,则梯形面积S梯形ABCD=
20、如图,在梯形ABCD中,AD∥BC,并且AB=8,AD=3,CD=6,并且∠B+∠C=90°,则梯形面积S梯形ABCD=