题目内容
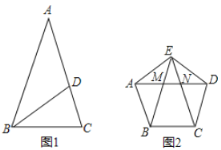
【题目】（1）如图1，已知△ABC中AB=AC，∠BAC=36°，BD是角平分线，求证：点D是线段AC的黄金分割点；
（2）如图2，正五边形的边长为2，连结对角线AD、BE、CE，线段AD分别与BE和CE相交于点M、N，求MN的长；
（3）设⊙O的半径为r，直接写出它的内接正十边形的长=_________________（用r的代数式表示）．
【答案】（1）详见解析；（2）
；（3）
【解析】
（1）根据等腰三角形的性质可得
，再通过证明
可得
，即
，即可证明点D是线段AC的黄金分割点；
（2）根据正五边形的性质求得
，
，根据相似比
，即可求出MN的长；
（3）设AB是圆内接正十边形的边长，连接OA、OB，作∠OAB的角平分线交OB于C，通过证明
得出比例式，即可求出答案．
（1）∵AB=AC，∠BAC=36°
∴
∵BD是
的角平分线
∴
∴
∴
∴
∴
，
∴
∴
∴
∴点D是线段AC的黄金分割点．
（2）∵
∴
∴
，
∴
，
∴
，
∴
∴
，
∴
∴
∴
∴
∴
解得
或
（舍去）
故MN的长为
．
（3）设AB是圆内接正十边形的边长，连接OA、OB，作∠OAB的角平分线交OB于C
则
，
，
∴
∵
∴
∴
∵
，
∴
∴
∵
∴
解得
或
（舍去）
经检验当时，
，所以根成立
故．
练习册系列答案
名校课堂系列答案
相关题目
