题目内容
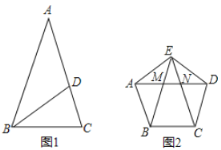
【题目】如图1,抛物线y=﹣x2﹣2x+3与x轴从左到右交于A、B两点,与y轴交于点C,顶点为D

(1)求直线AC的解析式与点D的坐标;
(2)在直线AC上方的抛物线上有一点E,作EF∥x轴,与抛物线交于点F,作EM⊥x轴于M,作FN⊥x轴于N,长度为2![]() 的线段PQ在直线AC上运动(点P在点Q右侧),当四边形EMNF的周长取最大值求四边形DPQE的周长的最小值及对应的点Q的坐标;
的线段PQ在直线AC上运动(点P在点Q右侧),当四边形EMNF的周长取最大值求四边形DPQE的周长的最小值及对应的点Q的坐标;
(3)如图2,平移抛物线,使抛物线的顶点D在直线AD上移动,点D平移后的对应点为D′,点A平移后的对应点为A′,△A′D′C是否能为直角三角形?若能,请求出对应的线段D′C的长;若不能,请说明理由.
【答案】(1)直线AC的解析式为:![]() ,
,![]() ;(2)四边形DPQE的周长的最小值是
;(2)四边形DPQE的周长的最小值是![]() ,对应的点Q的坐标为
,对应的点Q的坐标为![]() ;(3)
;(3)![]() =
=![]() 或
或![]() 或3.
或3.
【解析】
(1)抛物线![]() 与x轴从左到右交于A、B两点,只要令y=0,即可求出A、B两点;与y轴交于点C,只要令x=0,即可求出点C;由点A、C的坐标可得直线AC的解析;D的坐标用顶点公式或者先求出对称轴代入解析式,即可求出;
与x轴从左到右交于A、B两点,只要令y=0,即可求出A、B两点;与y轴交于点C,只要令x=0,即可求出点C;由点A、C的坐标可得直线AC的解析;D的坐标用顶点公式或者先求出对称轴代入解析式,即可求出;
(2)作点E关于直线AC的对称点E'(0,1),将点E'沿AC方向平移![]() 个单位得到E″(2,3),连接E″D交直线AC于点P,将点P向下平移
个单位得到E″(2,3),连接E″D交直线AC于点P,将点P向下平移![]() 个单位得到Q,则点Q为所求点即可求解,再根据个点坐标求出四边形的边长,进而计算周长;
个单位得到Q,则点Q为所求点即可求解,再根据个点坐标求出四边形的边长,进而计算周长;
(3)分A'D'是斜边、A'C是斜边、CD'是斜边三种情况,分别求解即可.
解:(1)∵抛物线![]() 与x轴从左到右交于A、B两点,
与x轴从左到右交于A、B两点,
∴令y=0,即![]() ,解得:
,解得:![]() ,则
,则![]()
∵抛物线![]() 与y轴交于点C,
与y轴交于点C,
∴![]()
由点A、C的坐标得,直线AC的解析式为:![]() ;
;
∵D是抛物线![]() 的顶点,抛物线的对称轴为:
的顶点,抛物线的对称轴为:![]() ,
,
∴![]() ;
;
(2)设点![]() ,
,
∵抛物线的对称轴为:![]() ,
,![]() 轴,
轴,
∴![]()
四边形![]() 的周长
的周长![]() ,
,
当![]() 时,
时,![]() 最大,此时点
最大,此时点![]() ;
;
∵![]() ,
,![]() ;
;
∴![]() ;
;
∵![]() 且P、Q在
且P、Q在![]() 上
上
∴P、Q两点横纵坐标差为2,
作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,将点
,将点![]() 沿
沿![]() 方向平移
方向平移![]() 个单位得到
个单位得到![]() ,
,
由点![]() 坐标得,直线
坐标得,直线![]() 的解析式为:
的解析式为:![]() ;
;
联立直线AC、直线![]() 的解析式并解得:
的解析式并解得:![]() ,故点
,故点![]() ,
,
将点![]() 沿着直线CA向左向下平移
沿着直线CA向左向下平移![]() 个单位得到点
个单位得到点![]() ;
;
∵![]() ,
,![]() ,
,![]() ,
,![]() ;
;
∴![]() ,
,![]() ;
;
此时四边形![]() 的周长最小
的周长最小
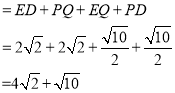 ;
;
(3)由待定系数法求得直线AD的解析式为:![]() ,则设抛物线向右平移m个单位,则向上平移2m个单位,
,则设抛物线向右平移m个单位,则向上平移2m个单位,
∴![]()
![]() 、
、![]()
![]() ,
,![]() ,
,
而点![]() ,
,
∴![]() ;
;
①当![]() 是斜边时,如图2,
是斜边时,如图2,
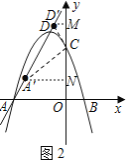
分别过点![]() 、
、![]() 作y轴的垂线交于点N、M,则
作y轴的垂线交于点N、M,则![]() ,
,
则![]() ,即
,即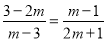 ,
,
解得:![]() (舍去)或
(舍去)或![]() ;
;
②当![]() 是斜边时,如图3,
是斜边时,如图3,
过点![]() 作x轴的平行线交y轴于点N,交过点
作x轴的平行线交y轴于点N,交过点![]() 作y轴的平行线于点M,
作y轴的平行线于点M,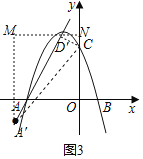
同理可得:![]() ,则
,则![]() ,
,
即![]() ,解得:
,解得:![]() ;
;
③当![]() 是斜边时,
是斜边时,
同理可得:![]() ,解得:
,解得:![]() ,
,
故![]() 或1或 1
或1或 1
则![]() =
=![]() 或
或![]() 或3.
或3.

 阅读快车系列答案
阅读快车系列答案