题目内容
 如图,直线y=
如图,直线y=| 3 |
| 4 |
考点:二次函数的最值,一次函数图象上点的坐标特征
专题:
分析:首先得出MN与x之间的函数关系,进而利用二次函数最值求法得出即可.
解答: 解:过点P分别作x轴、y轴的平行线坐标于点M、N,连接MN,
解:过点P分别作x轴、y轴的平行线坐标于点M、N,连接MN,
设P点坐标为:(x,
x+6),则NO2+MO2=NM2,
∴NM2=(
x+6)2+x2=
x2+9x+36,
此函数最小值为:
=
,
∵MN长度为正数,
∴MN=
.
故答案为:
.
 解:过点P分别作x轴、y轴的平行线坐标于点M、N,连接MN,
解:过点P分别作x轴、y轴的平行线坐标于点M、N,连接MN,设P点坐标为:(x,
| 3 |
| 4 |
∴NM2=(
| 3 |
| 4 |
| 25 |
| 16 |
此函数最小值为:
4×
| ||
4×
|
| 576 |
| 25 |
∵MN长度为正数,
∴MN=
| 24 |
| 5 |
故答案为:
| 24 |
| 5 |
点评:此题主要考查了二次函数最值求法,熟练记忆最值公式是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在2,0,-3.14,
各数中,无理数是( )
| 2 |
A、
| ||
| B、0 | ||
| C、-3.14 | ||
| D、2 |
 如图,茗茗从点O出发,先向东走15米,再向北走10米到达点M,如果点M的位置用(15,10)表示,那么(-10,5)表示的位置是( )
如图,茗茗从点O出发,先向东走15米,再向北走10米到达点M,如果点M的位置用(15,10)表示,那么(-10,5)表示的位置是( )| A、点A | B、点B | C、点C | D、点D |
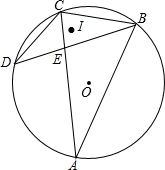 如图,已知△BAC,AB=AC,O为△ABC外心,D为⊙O上一点,BD与AC的交点为E,且BC2=AC•CE
如图,已知△BAC,AB=AC,O为△ABC外心,D为⊙O上一点,BD与AC的交点为E,且BC2=AC•CE 某公司想了解一款品牌运动服的销售情况来决定下一步的生产数量.该公司随机统计了某天各个摊位销售这款不同颜色的运动服的销售数量,并绘制成统计表和扇形统计图(如图).
某公司想了解一款品牌运动服的销售情况来决定下一步的生产数量.该公司随机统计了某天各个摊位销售这款不同颜色的运动服的销售数量,并绘制成统计表和扇形统计图(如图).