题目内容
 如图,在直角坐标平面上,点A(x1,-3)在第三象限,点B(x2,-1)在第四象限,线段AB交y轴于点D.∠AOB=90°,S△AOB=9,设∠AOD=α,求sinα•cosα的值.
如图,在直角坐标平面上,点A(x1,-3)在第三象限,点B(x2,-1)在第四象限,线段AB交y轴于点D.∠AOB=90°,S△AOB=9,设∠AOD=α,求sinα•cosα的值.分析:首先过点A作AC⊥x轴于C,过点B作BE⊥x轴于E,易得∠OAC=∠AOD=α,又由∠AOB=90°,易得∠BOE=∠AOD=α,即可得在Rt△AOC中,cosα=
,在Rt△BOE中,sinα=
,又由S△AOB=9,求得OA•OB的值,继而求得sinα•cosα的值.
| AC |
| OA |
| BE |
| OB |
解答: 解:过点A作AC⊥x轴于C,过点B作BE⊥x轴于E,
解:过点A作AC⊥x轴于C,过点B作BE⊥x轴于E,
∴AC∥y轴,
∴∠OAC=∠AOD=α,
∵∠AOB=90°,
∴∠AOD+∠BOD=90°,
∵∠BOD+∠BOE=90°,
∴∠BOE=∠AOD=α,
在Rt△AOC中,cosα=
,
在Rt△BOE中,sinα=
,
∵S△AOB=
OB•OA=9,
∴OB•OA=18,
∵A(x1,-3)点B(x2,-1),
∴sinα•cosα=
•
=
=
=
.
 解:过点A作AC⊥x轴于C,过点B作BE⊥x轴于E,
解:过点A作AC⊥x轴于C,过点B作BE⊥x轴于E,∴AC∥y轴,
∴∠OAC=∠AOD=α,
∵∠AOB=90°,
∴∠AOD+∠BOD=90°,
∵∠BOD+∠BOE=90°,
∴∠BOE=∠AOD=α,
在Rt△AOC中,cosα=
| AC |
| OA |
在Rt△BOE中,sinα=
| BE |
| OB |
∵S△AOB=
| 1 |
| 2 |
∴OB•OA=18,
∵A(x1,-3)点B(x2,-1),
∴sinα•cosα=
| AC |
| OA |
| BE |
| OB |
| AC•BE |
| OA•OB |
| 3 |
| 18 |
| 1 |
| 6 |
点评:此题考查了三角函数的定义、直角三角形的性质以及坐标与图形的性质.此题难度适中,解题的关键是准确作出辅助线,注意数形结合思想的应用.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
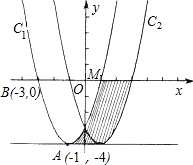 如图,在直角坐标平面xOy中,抛物线C1的顶点为A(-1,-4),且过点B(-3,0)
如图,在直角坐标平面xOy中,抛物线C1的顶点为A(-1,-4),且过点B(-3,0)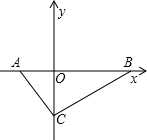 如图,在直角坐标平面中,Rt△ABC的斜边AB在x轴上,直角顶点C在y轴的负半轴上,cos∠ABC=
如图,在直角坐标平面中,Rt△ABC的斜边AB在x轴上,直角顶点C在y轴的负半轴上,cos∠ABC=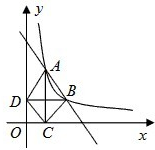 如图,在直角坐标平面内,函数y=
如图,在直角坐标平面内,函数y= 完成下列各题:
完成下列各题: 如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点C的坐标为(5,5),要使以A、B、C、D为顶点的四边形是平行四边形,且点D坐标在第一象限,那么点D的坐标是
如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点C的坐标为(5,5),要使以A、B、C、D为顶点的四边形是平行四边形,且点D坐标在第一象限,那么点D的坐标是