题目内容
1.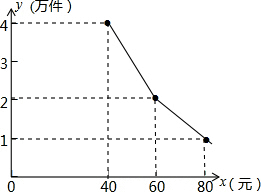 为扶持大学生自主创业,市政府提供了80万元的无息贷款,用于某大学生开办公司,生产并销售自主研发的一种电子产品,并约定用该公司的经营利润逐步偿还无息贷款,一盒子该产品的生产成本为每件40元;员工每人每月工资是2500元,公司每月支出其它费用15万元,该产品每月销售量y(万件)与销售单价x(元)之间的函数关系式如图所示.
为扶持大学生自主创业,市政府提供了80万元的无息贷款,用于某大学生开办公司,生产并销售自主研发的一种电子产品,并约定用该公司的经营利润逐步偿还无息贷款,一盒子该产品的生产成本为每件40元;员工每人每月工资是2500元,公司每月支出其它费用15万元,该产品每月销售量y(万件)与销售单价x(元)之间的函数关系式如图所示.(1)求月销售量y(万件)与销售单价x(元)之间的函数关系式;
(2)当销售单价定为50元时,为保证公司月利润达到5万元,该公司应安排员工多少人?
(3)若该公司有100名员工,则该公司最早可在几个月内还清无息贷款?
分析 (1)从图中看,这是一个分段一次函数,40≤x≤60和60<x<80时,函数的表达式不同,每段函数都经过两点,使用待定系数法即可求出函数关系式;
(2)利用(1)中的函数关系,当销售单价定为50元时,可计算出月销售量,设可安排员工a人,利润=销售额一生产成本-员工工资-其它费用,列出方程即可解;
(3)先分情况讨论出利润的最大值,即可求解.
解答 解:(1)当40≤x≤60时,令y=kx+b,
则$\left\{\begin{array}{l}{40k+b=4}\\{60k+b=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-0.1}\\{b=8}\end{array}\right.$.
故y=-0.1x+8,
同理,当60<x<80时,y=-0.05x+5.
故y=$\left\{\begin{array}{l}{-0.1x+8(40≤x≤60)}\\{-0.05x+5(60<x≤80)}\end{array}\right.$;
(2)设公司可安排员工a人,定价50元时,
由5=(-0.1×50+8)(50-40)-15-0.25a,
得30-15-0.25a=5,
解得a=40.
所以公司可安排员工40人;
(3)当40≤x≤60时,
利润w1=(-0.1x+8)(x-40)-15-20=-0.1(x-60)2+5,
则当x=60时,wmax=5万元;
当60<x≤100时,
w2=(-0.05x+5)(x-40)-15-0.25×80
=-0.05(x-70)2+10,
∴x=70时,wmax=10万元,
∴要尽早还清贷款,只有当单价x=70元时,获得最大月利润10万元,
设该公司n个月后还清贷款,则10n≥80,
∴n≥8,即n=8为所求.
点评 此题主要考查二次函数的运用,利用待定系数法求解一次函数关系式,一次函数与一次不等式的应用,是一道综合性较强的代数应用题,能力要求比较高.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案| A. | y=0.2x+18.5(1≤x≤6) | B. | y=0.2x+18.7(1≤x≤6) | ||
| C. | y=0.2x+22(1≤x≤6) | D. | y=0.2x+22.2(1≤x≤6) |
| A. | (-a2)3=a6 | B. | (a+b)2=a2+b2 | C. | $\root{3}{-64}$=-4 | D. | 5$\sqrt{5}$-$\sqrt{5}$=4 |
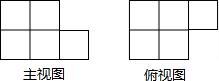 如图,由几个相同的小正方体搭成的几何体的主视图和俯视图,组成这个几何体的小正方体的个数最多是( )
如图,由几个相同的小正方体搭成的几何体的主视图和俯视图,组成这个几何体的小正方体的个数最多是( )| A. | 7个 | B. | 8个 | C. | 9个 | D. | 10个 |
| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
| 时间 | 0:00 | 4:00 | 8:00 | 12:00 | 16:00 | 20:00 |
| 气温 | 18℃ | 17℃ | 19℃ | 26℃ | 27℃ | 22℃ |
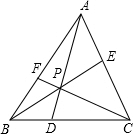 如图,在△ABC内任取一点P,连接并延长AP、BP、CP,分别交对边于点D、E、F,则$\frac{PD}{AD}$+$\frac{PE}{BE}$+$\frac{PF}{CF}$=1.
如图,在△ABC内任取一点P,连接并延长AP、BP、CP,分别交对边于点D、E、F,则$\frac{PD}{AD}$+$\frac{PE}{BE}$+$\frac{PF}{CF}$=1.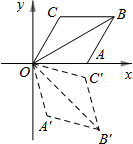 如图,菱形OABC的一边OA在x轴上,将菱形OABC绕原点O顺时针旋转75°至菱形OA′B′C′的位置.若OB=2$\sqrt{3}$,∠C=120°,则点B′的坐标为($\sqrt{6}$,-$\sqrt{6}$).
如图,菱形OABC的一边OA在x轴上,将菱形OABC绕原点O顺时针旋转75°至菱形OA′B′C′的位置.若OB=2$\sqrt{3}$,∠C=120°,则点B′的坐标为($\sqrt{6}$,-$\sqrt{6}$).