题目内容
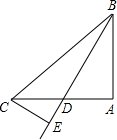 已知∠A=90°,AB=AC,BD平分∠ABC,CE⊥BD,垂足为E,则
已知∠A=90°,AB=AC,BD平分∠ABC,CE⊥BD,垂足为E,则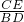 =________.
=________.

分析:延长CE、BA交于F点,由BD平分∠ABC,CE⊥BD,可证E为CF的中点,由AB=AC,利用互余关系证明△ACF≌△ABD,得出CF=BD,利用线段的关系得出结论.
解答:
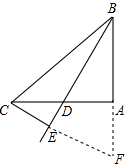 解:延长CE、BA交于F点,
解:延长CE、BA交于F点,∵BD平分∠ABC,CE⊥BD,
∴CE=
 CF,
CF,又∵∠CED=∠DAB=90°,∠CDE=∠ADB,
∴∠ECD=∠ABD,而AB=AC,
∴△ACF≌△ABD,
∴CF=BD,
∴
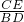 =
=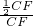 =
= .
.故答案为:
 .
.点评:本题考查了三角形全等的判定与性质.关键是根据已知条件得出等腰三角形底边上的“三线合一”,利用互余关系证明三角形全等.

练习册系列答案
相关题目
在Rt△ABC中,已知∠C=90°,AC=3,BC=4,那么∠A的余切值等于 ( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 ,1).
,1). (2012•郑州模拟)如图,△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD.把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m=
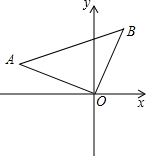
(2012•郑州模拟)如图,△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD.把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m= 在平面直角坐标系中,△AOB的位置如图所示.已知∠AOB=90°,AO=BO,点A的坐标为(-3,1).
在平面直角坐标系中,△AOB的位置如图所示.已知∠AOB=90°,AO=BO,点A的坐标为(-3,1). 如图,已知∠AOC=90°,下列说法正确的有( )
如图,已知∠AOC=90°,下列说法正确的有( )