题目内容
（2012•郑州模拟）如图，△ABC中，已知∠C=90°，∠B=55°，点D在边BC上，BD=2CD．把△ABC绕着点D逆时针旋转m（0＜m＜180）度后，如果点B恰好落在初始Rt△ABC的边上，那么m=70°或120°
70°或120°
．分析：根据点B所落的边不同，分①点B落在AB边上时，根据旋转的性质可得BD=BD′，然后利用等腰三角形的两底角相等列式求出∠BDB′的度数，即可得到旋转角m；②点B落在AC上时，根据旋转的性质可得BD=BD′，然后根据直角三角形30°角所对的直角边等于斜边的一半求出∠CB′D，再根据直角三角形两锐角互余求出∠CDB′，然后求出∠BDB′，即可得到旋转角m．
解答：
解：①如图1，点B落在AB边上时，根据旋转的性质可得BD=BD′，
∵∠B=55°，
∴∠BDB′=180°-2×55°=180°-110°=70°，
即m=70°；
②如图2，点B落在AC上时，根据旋转的性质可得BD=BD′，
∵BD=2CD，
∴B′D=2CD，
∴∠CB′D=30°，
在Rt△B′CD中，∠CDB′=90°-30°=60°，
∠BDB′=180°-60°=120°，
即m=120°，
综上所述，m=70°或120°．
故答案为：70°或120°．
解：①如图1，点B落在AB边上时，根据旋转的性质可得BD=BD′，∵∠B=55°，
∴∠BDB′=180°-2×55°=180°-110°=70°，
即m=70°；
②如图2，点B落在AC上时，根据旋转的性质可得BD=BD′，
∵BD=2CD，
∴B′D=2CD，
∴∠CB′D=30°，
在Rt△B′CD中，∠CDB′=90°-30°=60°，
∠BDB′=180°-60°=120°，
即m=120°，
综上所述，m=70°或120°．
故答案为：70°或120°．
点评：本题考查了旋转的性质，主要利用了等腰三角形两个底角相等，直角三角形30°角所对的直角边等于斜边的一半的性质，要注意分点B落在AB、AC两条边上分情况讨论求解．
练习册系列答案
相关题目
（2012•郑州模拟）将两张矩形纸片如图所示摆放，使其中一张矩形纸片的一个顶点恰好落在另一张矩形纸片的一条边上，若∠1=26°，则∠2的度数为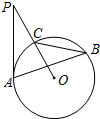
（2012•郑州模拟）如图，PA与⊙O相切，切点为A，PO交⊙O于点C，点B是优弧
（2012•郑州模拟）郑州地铁一号线将于2013年底建成，它的通车将给市民的出行方式带来一些新变化．小王和小林准备利用课余时间，以问卷的方式对郑州市民的出行方式进行调查．如图是郑州地铁一号线图（部分），小王和小林分别从郑州火车站、二七广场站、市体育馆站这三站中，随机选取一站向其周围的人群进行问卷调查，则小王选取的站点与小林选取的站点相邻的概率是
（2012•郑州模拟）已知二次函数y=ax2+bx-2的图象经过点A（1，0）及B（-2，0）两点．