题目内容
探究一:如图1,已知正方形ABCD,E、F分别是BC、AB上的两点,且AE⊥DF.小明经探究,发现AE=DF.请你帮他写出证明过程.
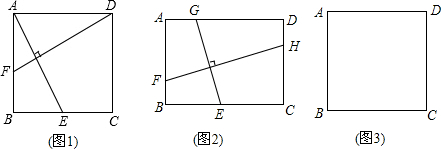
探究二:如图2,在矩形ABCD中,AB=3,BC=4,E、G分别在边BC、AD上,F、H分别在边AB、CD上,且GE⊥FH.小明发现,GE与FH并不相等,请你帮他求出
的值.
探究三:小明思考这样一个问题:如图3,在正方形ABCD中,若E、G分别在边BC、AD上,F、H分别在边AB、CD上,且GE=FH,试问:GE⊥FH是否成立?若一定成立,请给予证明;若不一定成立,请画图并作出说明.

探究二:如图2,在矩形ABCD中,AB=3,BC=4,E、G分别在边BC、AD上,F、H分别在边AB、CD上,且GE⊥FH.小明发现,GE与FH并不相等,请你帮他求出
| GE |
| FH |
探究三:小明思考这样一个问题:如图3,在正方形ABCD中,若E、G分别在边BC、AD上,F、H分别在边AB、CD上,且GE=FH,试问:GE⊥FH是否成立?若一定成立,请给予证明;若不一定成立,请画图并作出说明.
考点:四边形综合题
专题:
分析:探究一、求出∠ADF=∠BAE,∠DAF=∠ABE=90°,求出△ADF≌△DAE即可;
探究二、作GM⊥BC于M,FN⊥CD于N,证出△GME∽△FNH即可;
探究三、画出图形,即可得出答案.
探究二、作GM⊥BC于M,FN⊥CD于N,证出△GME∽△FNH即可;
探究三、画出图形,即可得出答案.
解答:探究一
证明:∵四边形ABCD是正方形,
∴∠DAF=∠ABE=90°,AD=AB,
∴∠DAE+∠BAE=90°,
∵AE⊥DF,
∴∠DAE+∠ADF=90°,
∴∠ADF=∠BAE,
在△ADF和△BAE中,
,
∴△ADF≌△DAE(ASA),
∴AE=DF;
探究二、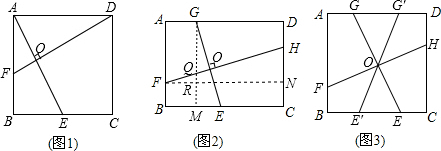
解:作GM⊥BC于M,FN⊥CD于N,如图2,
则GM=AB=3,FN=AD=4,∠GME=∠FNH=∠GOF=90°,
∴∠EGM+∠GQO=90°,∠HFN+∠FQR=90°,
∵∠FQR=∠GQO,
∴∠HFN=∠EGM,
∵∠GME=∠FNH,
∴△GME∽△FNH,
∴
=
,
又∵AB=GM=3,FN=BC=4,
∴
=
;
探究三、
解:不一定成立,如图3,当在GE时,GE和FH垂直,当在G′E′时,G′E′和FH就不垂直.
证明:∵四边形ABCD是正方形,
∴∠DAF=∠ABE=90°,AD=AB,
∴∠DAE+∠BAE=90°,
∵AE⊥DF,
∴∠DAE+∠ADF=90°,
∴∠ADF=∠BAE,
在△ADF和△BAE中,
|
∴△ADF≌△DAE(ASA),
∴AE=DF;
探究二、

解:作GM⊥BC于M,FN⊥CD于N,如图2,
则GM=AB=3,FN=AD=4,∠GME=∠FNH=∠GOF=90°,
∴∠EGM+∠GQO=90°,∠HFN+∠FQR=90°,
∵∠FQR=∠GQO,
∴∠HFN=∠EGM,
∵∠GME=∠FNH,
∴△GME∽△FNH,
∴
| GE |
| FH |
| GM |
| FN |
又∵AB=GM=3,FN=BC=4,
∴
| GE |
| FH |
| 3 |
| 4 |
探究三、
解:不一定成立,如图3,当在GE时,GE和FH垂直,当在G′E′时,G′E′和FH就不垂直.
点评:本题考查了矩形性质,全等三角形的性质和判定,相似三角形的性质和判定的应用,主要考查学生的推理能力.

练习册系列答案
相关题目
下列计算中,正确的是( )
A、
| ||||||||||
B、-a
| ||||||||||
C、
| ||||||||||
D、-
|
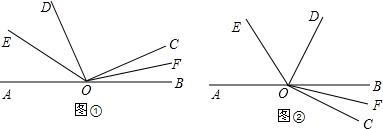
下图的角可以用∠O来表示的是( )
A、 |
B、 |
C、 |
D、 |
小颖按如图所示的程序输入一个正整数x,最后输出的结果为656,则满足条件的x的不同值有( )个.


| A、1 | B、2 | C、3 | D、4 |
要使4x2+25y2能变为一个完全平方式,则应加入的一项可以是( )
| A、10xy |
| B、20xy |
| C、-20xy |
| D、20xy或-20xy |
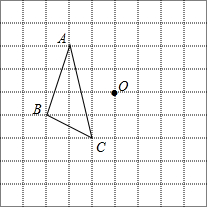 如图,三角形ABC是格点三角形(点A、B、C都在格点上),点O也在格点上.
如图,三角形ABC是格点三角形(点A、B、C都在格点上),点O也在格点上. 已知二次函数y=-x2+4x+5,完成下列各题:
已知二次函数y=-x2+4x+5,完成下列各题: