题目内容
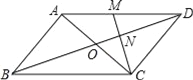
【题目】已知：在
中，
，
，点
为
的中点.
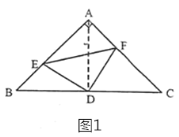
（1）如图1，
、
分别是
、
上的点，且
，求证：
为等腰直角三角形.
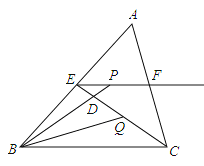
（2）如图2，若、分别为，
延长线上的点，仍有，其他条件不变，那么，是否仍为等腰直角三角形？证明你的结论.
【答案】(1)见解析;(2)见解析.
【解析】
（1）先连接AD，构造全等三角形：△BED和△AFD．AD是等腰直角三角形ABC底边上的中线，所以有∠CAD=∠BAD=45°，AD=BD=CD，而∠B=∠C=45°，所以∠B=∠DAF，再加上BE=AF，AD=BD，可证出：
，从而得出DE=DF，∠BDE=∠ADF，从而得出∠EDF=90°，即△DEF是等腰直角三角形；
（2）还是证明：
，主要证∠DAF=∠DBE（∠DBE=180°-45°=135°，∠DAF=90°+45°=135°），再结合两组对边对应相等，所以两个三角形全等．
（1）证明：连结
，如图1所示，
∵
，
，
为
的中点，
∴
，
，
∴
，
又
，
∴
.
∴
，
，
∴
.
∴
为等腰直角三角形；
（2）若
、
分别是
、
延长线上的点，连结，如图2所示，
∵，，为的中点，
∴
，，
∴
，
∴
.
又
，
∴
，
∴
，
，
∴
.
∴仍为等腰直角三角形.
练习册系列答案
相关题目
