题目内容
11.先化简:$\frac{{{a^2}-{b^2}}}{{{a^2}-ab}}÷({a+\frac{{2ab+{b^2}}}{a}})$,当b=-1时,再从-2<a<2的范围内选取一个合适的整数a代入求值.分析 先根据分式混合运算的法则把原式进行化简,再选出合适的a的值代入进行计算即可.
解答 解:原式=$\frac{(a+b)(a-b)}{a(a-b)}÷\frac{{{a^2}+2ab+{b^2}}}{a}$
=$\frac{1}{a+b}$,
在-2<a<2中,a可取的整数为-1、0、1,而当b=-1时,
①若a=-1,分式$\frac{{{a^2}-{b^2}}}{{{a^2}-ab}}$无意义;
②若a=0,分式$\frac{{2ab+{b^2}}}{a}$无意义;
③若a=1,分式$\frac{1}{a+b}$无意义.
所以a在规定的范围内取整数,原式均无意义(或所求值不存在).
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
1.某学习小组7位同学,为地震灾区捐款,捐款金额分别为5元、6元、6元、6元、7元、8元、9元,则这组数据的中位数与众数分别为( )
| A. | 6,6 | B. | 7,6 | C. | 7,8 | D. | 6,8 |
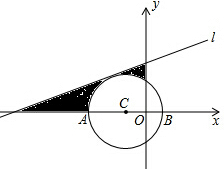 已知:如图,以C(-1,0)为圆心,2为半径的圆与x轴交于A、B,直线l的解析式为y=$\frac{\sqrt{3}}{3}$x+$\frac{5\sqrt{3}}{3}$
已知:如图,以C(-1,0)为圆心,2为半径的圆与x轴交于A、B,直线l的解析式为y=$\frac{\sqrt{3}}{3}$x+$\frac{5\sqrt{3}}{3}$ 已知,如图,在△ABC中,∠BAC=80°,AD⊥BC于D,AE平分∠DAC,∠B=60°,求∠AED.
已知,如图,在△ABC中,∠BAC=80°,AD⊥BC于D,AE平分∠DAC,∠B=60°,求∠AED.