题目内容
某汽车销售公司6月份销售某厂家的汽车,在一定范围内,每部汽车的进价与销售量有如下关系:若当月仅售出1部汽车,则该部汽车的进价为27万元,每多售出1部,所有售出的汽车的进价均降低0.1万元/部,月底厂家根据销售量一次性返利给销售公司,销售量在10部以内(含10部),每部返利0.5万元;销售量在10部以上,每部返利1万元.
(1)若该公司当月售出3部汽车,则每部汽车的进价为 万元;
(2)如果汽车的售价为28万元/部,该公司计划当月返利12万元,那么需要售出多少部汽车?(盈利=销售利润+返利)
(1)24.78;(2)6.
【解析】
试题分析:分析:(1)根据若当月仅售出1部汽车,则该部汽车的进价为27万元,每多售出1部,所有售出的汽车的进价均降低0.1万元/部,得出该公司当月售出4部汽车时,则每部汽车的进价为:27-0.1×2,即可得出答案;
(2)利用设需要售出x部汽车,由题意可知,每部汽车的销售利润,根据当0≤x≤10,以及当x>10时,分别讨论得出即可.
试题解析:(1)∵若当月仅售出1部汽车,则该部汽车的进价为27万元,每多售出1部,所有售出的汽车的进价均降低0.1万元/部,
∴若该公司当月售出3部汽车,则每部汽车的进价为:27-0.1×(4-1)=24.78,
(2)设需要售出x部汽车,
由题意可知,每部汽车的销售利润为:
28-[27-0.1(x-1)]=(0.1x+0.9)(万元),
当0≤x≤10,
根据题意,得x•(0.1x+0.9)+0.5x=12,
整理,得x2+14x-120=0,
解这个方程,得x1=-20(不合题意,舍去),x2=6,
当x>10时,
根据题意,得x•(0.1x+0.9)+x=12,
整理,得x2+19x-120=0,
解这个方程,得x1=-24(不合题意,舍去),x2=5,
因为5<10,
所以x2=5舍去.
答:需要售出6部汽车.
考点:一元二次方程的应用 .

 阅读快车系列答案
阅读快车系列答案 化成一般形式为 .
化成一般形式为 .



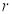 为半径的圆上有且仅有两点到
为半径的圆上有且仅有两点到 轴所在直线的距离等于1,则圆的半径
轴所在直线的距离等于1,则圆的半径 B.
B. C.
C. D.
D.


 ,3)、(﹣
,3)、(﹣ ,4)
,4)  ,4)
,4)  ,
, )、(﹣
)、(﹣ ,4)
,4)  ,4)
,4)