题目内容
已知a、b、c为△ABC的三边,a,b是x2-(c+4)x+4c+8=0的两根,
①判断△ABC的形状;
②若5a=3c,求a、b、c的长.
解:①∵a,b是x2-(c+4)x+4c+8=0的两根,∴a+b=-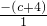 =c+4,ab=
=c+4,ab= =4c+8,
=4c+8,
∴a2+b2=(a+b)2-2ab=(c+4)2-2(4c+8)=c2,
∴△ABC是直角三角形;
②∵5a=3c,∴a= c,∵a+b=c+4,∴b=
c,∵a+b=c+4,∴b= c+4,
c+4,
∵ab=4c+8,∴3c2-20c-100=0,
解得c=10或- (舍去),
(舍去),
∴a= ×10=6,b=
×10=6,b= ×10+4=8.
×10+4=8.
分析:①由根与系数的关系,求得a+b=c+4,ab=4c+8,再求得a2+b2,从而判断出△ABC的形状;
②由①得到的两个关系式a+b=c+4,ab=4c+8,及5a=3c组成方程组,求解即可.
点评:本题考查了一元二次方程根与系数的关系以及勾股定理的逆定理.
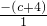 =c+4,ab=
=c+4,ab= =4c+8,
=4c+8,∴a2+b2=(a+b)2-2ab=(c+4)2-2(4c+8)=c2,
∴△ABC是直角三角形;
②∵5a=3c,∴a=
 c,∵a+b=c+4,∴b=
c,∵a+b=c+4,∴b= c+4,
c+4,∵ab=4c+8,∴3c2-20c-100=0,
解得c=10或-
 (舍去),
(舍去),∴a=
 ×10=6,b=
×10=6,b= ×10+4=8.
×10+4=8.分析:①由根与系数的关系,求得a+b=c+4,ab=4c+8,再求得a2+b2,从而判断出△ABC的形状;
②由①得到的两个关系式a+b=c+4,ab=4c+8,及5a=3c组成方程组,求解即可.
点评:本题考查了一元二次方程根与系数的关系以及勾股定理的逆定理.

练习册系列答案
相关题目


 (1997•贵阳)已知:如图,CD为⊙O的直径,CD⊥AB,M为垂足,DM=2cm,弦AB=8cm,则⊙O的半径为
(1997•贵阳)已知:如图,CD为⊙O的直径,CD⊥AB,M为垂足,DM=2cm,弦AB=8cm,则⊙O的半径为 P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.