Question

（1）如果动点P（x，y）的坐标满足关系式试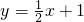，在表格中求出相对应的值，并在平面直角坐标系里描出这些点：

点的坐标	A	B	C	D	E
点的横坐标x		-2		2
点的纵坐标y	-1		1		3

（2）若将这五个点都先向右平移五个单位，再向上平移三个单位，至A₁、B₁、C₁、D₁、E₁，试分别写出它们的坐标．

Answer 1

解：（1）根据题意可得：
-1=x_A+1，得x_A=-4，
y_B=×（-2）+1，得y_B=0，
-1=x_C+1，得x_C=0，
y_D=×（-2）+1，得y_D=2，
-1=x_E+1，得x_E=4，
∴表格如下：

点的坐标	A	B	C	D	E
点的横坐标x	-4	-2	0	2	4
点的纵坐标y	-1	0	1	2	3

如下图：

（2）把（1）中点右平移五个单位，再向上平移三个单位得：
A₁（1，2），B₁（3，3），C₁（5，4），D₁（7，5），E₁（9，6）；
分析：（1）分别把相应点的坐标代入求值即可．
（2）根据几何变换思想，向右移动5个单位即x轴坐标加5，向上移动3个单位即y轴坐标加3，再根据（1）中求得的点的坐标即可得到平移后的点的坐标．
点评：本题考查了一次函数与几何变换，是基础题．