题目内容
如果动点P在坐标轴上，以点P为圆心，
为半径的圆与直线l：y=-
x+4相切，则满足条件的点P的个数是（ ）
| 12 |
| 5 |
| 4 |
| 3 |
| A、1个 | B、2个 | C、3个 | D、4个 |
分析：根据一次函数解析式得出函数图象，再利用直线与圆相切，即可得出答案．
解答：
解：∵y=-
x+4，
∴与x轴交于（3，0），与y轴交于（0，4），
∴点P为圆心，
为半径的圆与直线l：y=-
x+4相切，
∴符合要求的点的坐标有：（0，8），（0，0），（6，0）．
故选：C．
解：∵y=-| 4 |
| 3 |
∴与x轴交于（3，0），与y轴交于（0，4），
∴点P为圆心，
| 12 |
| 5 |
| 4 |
| 3 |
∴符合要求的点的坐标有：（0，8），（0，0），（6，0）．
故选：C．
点评：此题主要考查了直线与圆的位置之关系，正确得出函数图象是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
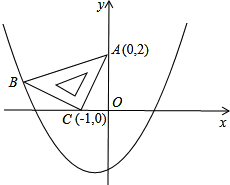两坐标轴上，且点A（0，2），点C（-1，0），如图所示；抛物线y=ax2+ax-2经过点B．
B转盘指针所指区域内的数字记为y．这样就确定了点P的坐标（x，y）．
为半径的圆与直线l：y=-
x+4相切，则满足条件的点P的个数是
为半径的圆与直线l：y=-
x+4相切，则满足条件的点P的个数是（ ）