题目内容
已知a、b、c满足 ,求:
,求:
(1)a、b、c的值;
(2)试问以a、b、c为边能否构成直角三角形?若能构成直角三角形,求出斜边上的高;若不能构成直角三角形,请说明理由.
解:(1)∵ ,
,
∴a- =0,b-5=0,c-
=0,b-5=0,c- =0,
=0,
∴a= ,b=5,c=
,b=5,c= ,
,
(2)∵a= ,b=5,c=
,b=5,c= ,
,
∴a2+c2=b2,
∴以a、b、c为边能构成直角三角形,
∴斜边上的高为:ac÷b=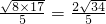 .
.
分析:(1)由非负数的性质:几个非负数相加为0,则都等于0.可求得a、b、c的值;
(2)根据勾股定理的逆定理可判断能否构成直角三角形,斜边上的高可用直角三角形的面积求解.
点评:本题考查勾股定理的逆定理的应用.综合考查了非负数的性质和直角三角形的面积求法.
 ,
,∴a-
 =0,b-5=0,c-
=0,b-5=0,c- =0,
=0,∴a=
 ,b=5,c=
,b=5,c= ,
,(2)∵a=
 ,b=5,c=
,b=5,c= ,
,∴a2+c2=b2,
∴以a、b、c为边能构成直角三角形,
∴斜边上的高为:ac÷b=
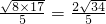 .
.分析:(1)由非负数的性质:几个非负数相加为0,则都等于0.可求得a、b、c的值;
(2)根据勾股定理的逆定理可判断能否构成直角三角形,斜边上的高可用直角三角形的面积求解.
点评:本题考查勾股定理的逆定理的应用.综合考查了非负数的性质和直角三角形的面积求法.

练习册系列答案
相关题目