Question

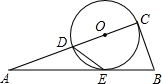（2013•河东区一模）如图，已知CD是⊙O的直径，AC⊥BC，垂足为C，点E为圆上一点，直线BE、CD相交于点A，且∠A+2∠AED=90°．
（Ⅰ）证明：直线AB是⊙O的切线；
（Ⅱ）当BC=1，AE=2，求tan∠OBC的值．

Answer 1

分析：（I）连接OE，CE，OB，求出BC=BE，证出△OEB≌△OCB，推出∠OEB=∠ACB=90°，根据切线的判定推出即可；
（II）证△AEO∽△ACB，推出

OE

BC

=

AE

AC

，求出

OE

BC

=

2

2

，解直角三角形求出即可．

解答：（Ⅰ）证明：连接OE，CE，OB，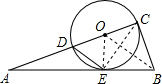
∵DC为圆O的直径，
∴∠DEC=90°，
即∠CEB+∠AED=90°，
∴2∠AED+∠2∠CEB=180°，
∵AC⊥BC，
∴∠ACB=90°，
∴∠A+∠ABC=90°，
∵∠A+2∠AED=90°，
∴∠ABC=2∠AED，
∴∠ABC+2∠CEB=180°，
∵∠ABC+∠CEB+∠ECB=180°，
∴∠CEB=∠ECB，
∴BC=BE，
在△OEB和△OCB中

BE=BC OE=OC OB=OB

，
∴△OEB≌△OCB，
∴∠OEB=∠ACB=90°，
即OE⊥AB，
∴AB是⊙O切线．

（Ⅱ）解：∵BE=BC=1，AB=2+1=3，
在Rt△ACB中，由勾股定理得：AC=

32-12

=2

2

，
∵∠A=∠A，∠AEO=∠ACB=90°，
∴△AEO∽△ACB，
∴

OE

BC

=

AE

AC

，
∴

OE

BC

=

2

2 2

=

2

2

，
∴tan∠OBC=

OC

BC

=

OE

BC

=

2

2

．

点评：本题考查了全等三角形的性质和判定，切线的判定和性质，相似三角形的性质和判定，解直角三角形的应用，主要考查学生综合运用性质进行推理和计算的能力．