题目内容
2.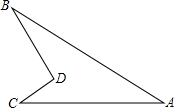 如图为一机器零件,∠A=36°的时候是合格的,小明测得∠BDC=98°,∠C=38°,∠B=23°.
如图为一机器零件,∠A=36°的时候是合格的,小明测得∠BDC=98°,∠C=38°,∠B=23°.请问该机器零件是否合格并说明你的理由.
分析 作直线AD,根据三角形的外角性质可得:∠3=∠B+∠1,∠4=∠C+∠2,从而推出∠BAC=∠1+∠2=∠3+∠4-∠B-∠D=37°.
解答  解:作直线AD,
解:作直线AD,
∴∠3=∠B+∠1---(1)
∴∠4=∠C+∠2---(2)
由(1)、(2)得:∠3+∠4=∠B+∠C+∠1+∠2,
即∠BDC=∠B+∠C+∠BAC,
∵∠BDC=98°,∠C=38°,∠B=23°
∴∠BAC=98°-38°-23°=37°≠36°,
∴该机器零件不合格.
点评 本题考查的是三角形外角的性质,解答此题的关键是构造三角形,应用三角形内角与外角的关系解答.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
7.化简:-$\sqrt{(1-sin52°)^{2}}$-$\sqrt{(1-tan52°)^{2}}$的结果是( )
| A. | tan52°-sin52° | B. | sin52°-tan52° | C. | 2-sin52°-tan52° | D. | -sin52°-tan52° |
7.若实数x,y满足$\frac{1}{2}$y-xy+x2+2=0,则实数y满足的条件是( )
| A. | y≤-2 | B. | y≥4 | C. | y2-2y-8≥0 | D. | 一切实数 |
14.当式子|x-1|+|x-2|+|x-3|+…+|x-2015|取得最小值时,实数x的值等于( )
| A. | 2015 | B. | 2014 | C. | 1009 | D. | 1008 |