题目内容
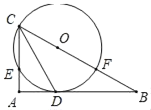
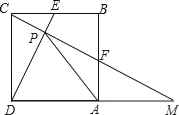
【题目】如图,在正方形ABCD中,E、F分别是CB,AB的中点,连接CF并延长,与DA的延长线交于点M,连接DE交CF于点P,连接AP,则有下列结论:①∠BCF=∠CDE;②AP=AD:③CM=CD+DE;④S△CDM=5S四边形EPFB,其中正确的结论有( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
根据正方形的性质,即可得∠DCE=∠B=90°,CD=BC=AB,又由E、F分别是CB,AB的中点,利用SAS即可判定△DCE≌△CBF,根据全等三角形的对应边相等,即可判定①正确;根据全等三角形对应角相等,即可得DE⊥CF,再利用ASA证得△BCF≌△AMF,即可得到AD=AM,然后利用直角三角形斜边上的中线等于斜边的一半,即可判定②正确;由△DCE≌△CBF,可得CF=DM,根据直角三角形的性质,可得FM>AM,即FM>CD,可判定③错误;利用相似三角形的性质:相似三角形的面积比等于相似比的平方,即可判定④正确.
解:∵四边形ABCD是正方形,
∴∠DCE=∠B=90°,CD=BC=AB,
∵E、F分别是CB,AB的中点,
∴BF=![]() AB,CE=
AB,CE=![]() BC,
BC,
∴BF=CE,
∴△DCE≌△CBF(SAS),
∴∠BCF=∠CDE,
故①正确;
∵∠CDE+∠CEP=90°,
∴∠BCF+∠CEP=90°,
∴∠CPE=90°,
即CF⊥DE,
∵BF=AF,∠B=∠BAM=90°,∠BFC=∠AFM,
∴△BCF≌△AMF(ASA),
∴AM=BC,
∴AD=AM,
∴AP=AD,
故②正确;
∵△DCE≌△CBF,
∴CF=DE,
∵∠FAM=90°,
∴FM>AM,
即FM>CD,
∴CM=CF+FM=DE+FM>CD+DE;
故③错误;
设CE=a,S△CDM=b,则BC=2a,AB=AD=AM=CD=2a,BF=AF=a,
∴MD=AD+AM=4a,
∴CF=![]() ,
,
∵∠BCF=∠PCE,∠B=∠CPE=90°,
∴△CPE∽△CBF,
∴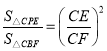 ,
,
∴S△CDM=5b,
∴S四边形EPFB=4b,
∵BC∥AD,
∴△CPE∽△MPD,
∴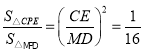 ,
,
∴S△MPD=16b,
∵![]() ,
,
∴S△CPD=4b,
∴S△CDM=S△CPD+S△MPD=4b+16b=20b,
∴S△CDM=5S四边形EPFB.
故④正确.
∴其中正确的结论有①②④.
故选:C.


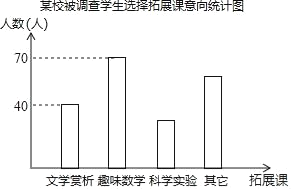
【题目】为丰富学生的课余生活,某校记划开展三种拓展课活动,分别是“文学赏析”,“趣味数学”,“科学实验”等项目,要求每位学生自主选择其中一项拓展课参加.随机抽取该校各年段部分学生,对选择拓展课的意向进行调査,将调查的结果制作成以下统计图和不完整的统计表.
某校被调查学生选择拓展课意向统计表
选择意向 | 所占百分比 |
文学赏析 |
|
趣味数学 | 35% |
科学实验 |
|
其它 | 30% |
(1)该校有2000名学生,请你估计大约有多少名学生参加科学实验拓展课,并补全统计表.
(2)该校参加科学实验拓展课的学生随机分成A,B,C三个人数相同的班级.小慧和小明都参加科学实验拓展课,求他们同班级的概率(画树状图或列表法求解)
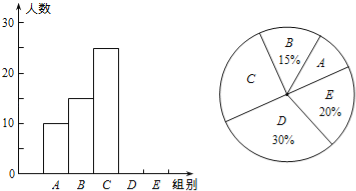
【题目】某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息解决下列问题:
(1)在统计表中,m= ,n= ,并补全条形统计图.
(2)扇形统计图中“C组”所对应的圆心角的度数是 .
(3)若该校共有900名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.