Question

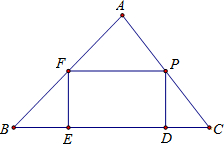
如图所示，P是△ABC边AC上的动点，以P为顶点作矩形PDEF，顶点D，E在边BC上，顶点F在边AB上；△ABC的底边BC及BC上的高的长分别为a，h，且是关于x的一元二次方程mx²+nx+k=0的两个实数根，设过D，E，F三点的⊙O的面积为S_⊙O，矩形PDEF的面积为S_矩形PDEF．
（1）求证：以a+h为边长的正方形面积与以a、h为边长的矩形面积之比不小于4；
（2）求

S⊙O

S矩形PDEF

的最小值；
（3）当

S⊙O

S矩形PDEF

的值最小时，过点A作BC的平行线交直线BP与Q，这时线段AQ的长与m，n，k的取值是否有关？请说明理由．

Answer 1

分析：（1）由根与系数的关系可得到a+h及ah的值，然后分别表示出正方形和矩形的面积，再根据根的判别式进行判断即可；
（2）过D、E、F三点的⊙O一定是以DF为直径的圆，那么其面积为：

π

4

（EF²+DE²）；而矩形PDEF的面积为：EF•DE；那么

S⊙O

S矩形PDEF

=

π

4

(

EF

DE

+

DE

EF

)，可将

EF

DE

看作一个整体，将两个图形的面积比转化为完全平方式，进而得出其最小值；
（3）过B作BM⊥AQ于M，交直线PF于N；易证得△FBP∽△ABQ，根据相似三角形的对应线段成比例可得EP：AQ=BN：BM；而当（2）的面积比最小时，EF=DE，此时BN=FP，即AQ=BM=h；h是已知方程的一个根，由此可判断出AQ的长是否与m、n、k的取值有关．

解答：解：解法一：
（1）据题意，∵a+h=-

n

m

，ah=

k

m

∴所求正方形与矩形的面积之比：

(a+h)2

ah

=

(- n m )2

k m

=

n2

mk

（1分）
∵n²-4mk≥0，∴n²≥4mk，由ah=

k

m

知m，k同号，
∴mk＞0 （2分）
（说明：此处未得出mk＞0只扣（1分），不再影响下面评分）
∴

n2

mk

≥

4mk

mk

=4（3分）
即正方形与矩形的面积之比不小于4．

（2）∵∠FED=90°，∴DF为⊙O的直径．
∴⊙O的面积为：S⊙O=π(

DF

2

)2=π

DF2

4

=

π

4

(EF2+DE2)． （4分）
矩形PDEF的面积：S_矩形PDEF=EF•DE．
∴面积之比：

S⊙O

S矩形PDEF

=

π

4

(

EF

DE

+

DE

EF

)，设

EF

DE

=f．

S⊙O

S矩形PDEF

=

π

4

(f+

1

f

)
=

π

4

[(

f

)2+(

1

f

)2-2

f

-

1

f

+2

f

1

f

]
=

π

4

(

f

-

1

f

)2+

π

2

．（6分）
∵(

f

-

1

f

)2≥0，∴

π

4

(

f

-

1

f

)2+

π

2

≥

π

2

，
∴

f

=

1

f

，即f=1时（EF=DE），

S⊙O

S矩形PDEF

的最小值为

π

2

（7分）

（3）当

S⊙O

S矩形PDEF

的值最小时，这时矩形PDEF的四边相等为正方形．
过B点过BM⊥AQ，M为垂足，BM交直线PF于N点，设FP=e，
∵BN∥FE，NF∥BE，∴BN=EF，∴BN=FP=e．
由BC∥MQ，得：BM=AG=h．
∵AQ∥BC，PF∥BC，∴AQ∥FP，
∴△FBP∽△ABQ． （8分）
（说明：此处有多种相似关系可用，要同等分步骤评分）
∴

FP

AQ

=

BN

BM

，（9分）
∴

e

AQ

=

e

h

，∴AQ=h （10分）
∴AQ=

-n± n2-4mk

2m

（11分）
∴线段AQ的长与m，n，k的取值有关．
（解题过程叙述基本清楚即可）

解法二：
（1）∵a，h为线段长，即a，h都大于0，
∴ah＞0 （1分）（说明：此处未得出ah＞0只扣（1分），再不影响下面评分）
∵（a-h）²≥0，当a=h时等号成立．
故，（a-h）²=（a+h）²-4ah≥0．（2分）
∴（a+h）²≥4ah，
∴

(a+h)2

ah

≥4．（﹡） （3分）
这就证得

(a+h)2

a-h

≥4．（叙述基本明晰即可）
（2）设矩形PDEF的边PD=x，DE=y，则⊙O的直径为

x2+y2

．
S_⊙O=π(

x2+y2

2

)2（4分），S_矩形PDEF=xy

S⊙O

S矩形PDEF

=

π(x2+y2)

4xy

=

π

4

[

(x2+2xy+y2)-2xy

xy

]=

π

4

[

(x+y)2

xy

-2]（6分）

(x+y)2

xy

≥4由（1）（*）．
∴

π

4

[

(x+y)2

xy

-2]≥

π

4

(4-2)=

π

2

．
∴

S⊙O

S矩形PDEF

的最小值是

π

2

（7分）

（3）当

S⊙O

S矩形PDEF

的值最小时，
这时矩形PDEF的四边相等为正方形．
∴EF=PF．作AG⊥BC，G为垂足．
∵△AGB∽△FEB，∴

AB

BF

=

AG

EF

． （8分）
∵△AQB∽△FPB，

AB

BF

=

AQ

PF

，（9分）
∴

AB

BF

=

AG

EF

=

AQ

PF

．
而EF=PF，∴AG=AQ=h，（10分）
∴AG=h=

-n+ n2-4mk

2m

，
或者AG=h=

-n- n2-4mk

2m

（11分）
∴线段AQ的长与m，n，k的取值有关．
（解题过程叙述基本清楚即可）

点评：此题主要考查了矩形的性质、相似三角形的判定和性质以及二次函数的应用等知识，综合性强，难度较大．