题目内容
 如图,长方体的底面边长分别为1cm和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要
如图,长方体的底面边长分别为1cm和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要分析:将长方体展开,根据两点之间线段最短,可知所用细线最短长度.
解答: 解:将长方体展开,连接A、B,
解:将长方体展开,连接A、B,
根据两点之间线段最短,AB=
=10(cm);
如果从点A开始经过4个侧面缠绕n圈到达点B,
相当于直角三角形的两条直角边分别是8n和6,
根据勾股定理可知所用细线最短需要
=
=2
(cm).
故答案为:10;2
.
 解:将长方体展开,连接A、B,
解:将长方体展开,连接A、B,根据两点之间线段最短,AB=
| 82+62 |
如果从点A开始经过4个侧面缠绕n圈到达点B,
相当于直角三角形的两条直角边分别是8n和6,
根据勾股定理可知所用细线最短需要
| 62+(8n)2 |
| 36+64n2 |
| 9+16n2 |
故答案为:10;2
| 9+16n2 |
点评:本题考查了平面展开-最短路径问题,是一道趣味题,将长方体展开,根据两点之间线段最短,运用勾股定理解答即可.

练习册系列答案
相关题目
 如图,长方体的底面边长分别为3 cm和2 cm,高为6 cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要
如图,长方体的底面边长分别为3 cm和2 cm,高为6 cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要 如图,长方体的底面边长分别为1cm和3cm,高为6cm,如果用一根细线从点A开始经过4个侧面缠绕一圈到达B(B为棱的中点),那么所用细线最短需要多长?如果从点A开始经过4个侧面缠绕n圈到达点B,那么所用细线最短需要多长?
如图,长方体的底面边长分别为1cm和3cm,高为6cm,如果用一根细线从点A开始经过4个侧面缠绕一圈到达B(B为棱的中点),那么所用细线最短需要多长?如果从点A开始经过4个侧面缠绕n圈到达点B,那么所用细线最短需要多长?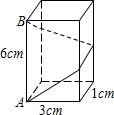 如图,长方体的底面边长分别为1cm 和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要
如图,长方体的底面边长分别为1cm 和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要 14、如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂奴爬行的最短路径长为
14、如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂奴爬行的最短路径长为