题目内容
如图,A、B是反比例函数y= (k>0)上得两个点,AC⊥x轴于点C,BD⊥y轴于点D,连接AD、BC,则△ABD与△ACB的面积大小关系是( )
(k>0)上得两个点,AC⊥x轴于点C,BD⊥y轴于点D,连接AD、BC,则△ABD与△ACB的面积大小关系是( )
A.S△ADB>S△ACB
B.S△ADB<S△ACB
C.S△ADB=S△ACB
D.不确定
【答案】分析:设A的横坐标是a,则纵坐标是 ,当B的横坐标是b时,则纵坐标是:
,当B的横坐标是b时,则纵坐标是: .利用三角形的面积公式即可求得两个三角形的面积,从而判断.
.利用三角形的面积公式即可求得两个三角形的面积,从而判断.
解答:解:设A的横坐标是a,则纵坐标是 ,
,
当B的横坐标是b时,则纵坐标是: .
.
则△ABD的面积是: b•(
b•( -
- )=
)= =
= ;
;
△ACB的面积是: •
• (b-a)=
(b-a)= .
.
故△ABD的面积=△ACB的面积.
故选C.
点评:本题是反比例函数与三角形的面积的综合应用,正确利用点的坐标表示出三角形的面积是关键.
 ,当B的横坐标是b时,则纵坐标是:
,当B的横坐标是b时,则纵坐标是: .利用三角形的面积公式即可求得两个三角形的面积,从而判断.
.利用三角形的面积公式即可求得两个三角形的面积,从而判断.解答:解:设A的横坐标是a,则纵坐标是
 ,
,当B的横坐标是b时,则纵坐标是:
 .
.则△ABD的面积是:
 b•(
b•( -
- )=
)= =
= ;
;△ACB的面积是:
 •
• (b-a)=
(b-a)= .
.故△ABD的面积=△ACB的面积.
故选C.
点评:本题是反比例函数与三角形的面积的综合应用,正确利用点的坐标表示出三角形的面积是关键.

练习册系列答案
相关题目
 如图所示,P是反比例函数图象在第二象限上的一点,且矩形PEOF的面积为3,则反比例函数的表达式是( )
如图所示,P是反比例函数图象在第二象限上的一点,且矩形PEOF的面积为3,则反比例函数的表达式是( )A、y=
| ||
B、y=
| ||
C、y=-
| ||
D、y=-
|
 如图,A、B是反比例函数y=
如图,A、B是反比例函数y=| k |
| x |
| A、S△ADB>S△ACB |
| B、S△ADB<S△ACB |
| C、S△ADB=S△ACB |
| D、不确定 |
 如图所示,P是反比例函数
如图所示,P是反比例函数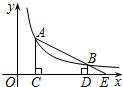 如图,A,B是反比例函数y=
如图,A,B是反比例函数y= 如图,若点P是反比例函数y=
如图,若点P是反比例函数y=