题目内容
已知东西海岸线上有相距7km的A、B两个码头，灯塔P距A码头13km，在B码头测得灯塔P在北偏东45°方向，则灯塔P到海岸线的距离为 km．
考点：解直角三角形的应用-方向角问题
专题：
分析：设PD=xkm，则AD=（7-x）cm．根据等腰直角三角形的性质和勾股定理进行解答．
解答：
解：设PD=xkm，则AD=（7-x）cm．
易证△BPD是等腰直角三角形，则PD=BD．
所以由勾股定理得：
=7-x，
整理，得
x2-7x-60=0，
解得 x=12（舍去负值）．
故答案是：12．
解：设PD=xkm，则AD=（7-x）cm．易证△BPD是等腰直角三角形，则PD=BD．
所以由勾股定理得：
| 132-x2 |
整理，得
x2-7x-60=0，
解得 x=12（舍去负值）．
故答案是：12．
点评：本题考查了解直角三角形的应用-方向角问题．将解直角三角形的相关知识有机结合，体现了数学应用于实际生活的思想．
练习册系列答案
相关题目
如图，将Rt△ABC绕直角顶点顺时针旋转90°，得到△A′B′C，连结AA′，若∠AA′B′=20°，则∠B的度数为
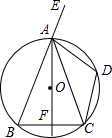如图，⊙O是△ABC的外接圆，AO⊥BC于F，D为 |
| AC |
| A、57° | B、38° |
| C、33° | D、28.5° |
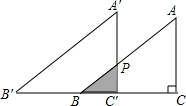如图所示，在Rt△ABC中，∠C=90°，BC=4cm，AC=3cm，若△A′B′C′与△ABC完全重合，令△ABC固定不动，将△A′B′C′沿CB所在的直线向左以1cm/s的速度移动．设移动xs后，△A′B′C′与△ABC的重合部分的面积为ycm2，求：