��Ŀ����
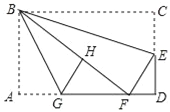
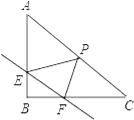
����Ŀ����ͼ����Rt��ABC�У���B=90�㣬ֱ��EF�ֱ���ֱ�DZ�AB��BC��E��F���㣬��EF��AC��P��б��AC���е㣬����PE��PF����AB=![]() ��BC=
��BC=![]() ��
��
��1����E��F��Ϊ��ֱ�DZߵ��е�ʱ����֤���ı���EPFB�Ǿ��Σ��������ʱEF�ij���
��2����EF�ij���Ϊx��x��0��������EPF=��Aʱ���ú�x�Ĵ���ʽ��ʾEP�ij���
��3�����PEF�����ΪS����EFΪ����ʱ��S�����ֵ������������ֵ��
���𰸡���1��֤����������EF=1;
��2����EP=![]() ��
��
��3���൱EF=1ʱ��S�����ֵΪ![]() ��
��
�������������������1��������ı���EPFB��ƽ���ı��Σ����ɡ�B=90���ó��ı���EPFB�Ǿ��Σ����ù��ɶ������EF��
��2��֤����APE�ס�PEF���ó���Ӧ�߳ɱ��������ɵó������
��3����FH��AC��AC�ڵ�H����EF=x���ó�BF��CF��FH��ֵ��������������������EF�����ֵ��������λ�߶����������EP��ֵ��
�����������1����ͼ1��
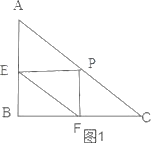
��E��AB���е㣬P��AC���е㣬
��EP��BC����EP=![]() BC��
BC��
��F��BC���е㣬
��EP��BF����EP=BF��
�ı���EPFB��ƽ���ı��Σ�
�ߡ�B=90����
���ı���EPFB�Ǿ��Σ�
��2����AB=![]() ��BC=
��BC=![]() ��
��
��BE=![]() ��BF=
��BF=![]() ��
��
��EF=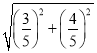 =1��
=1��
��2����EF��AC��
���APE=��PEF���ߡ�EPF=��A��
���APE�ס�PEF��
��![]() ��
��
��AP=1��EF=x��
��EP2=x��
��EP=![]() ��
��
��3����ͼ2����FH��AC��AC�ڵ�H��
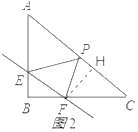
��EF��AC��
���BEF�ס�BAC��
��EF=x����BF=![]() x��CF=
x��CF=![]() ��
��![]() x��
x��
��FH=![]() CF=
CF=![]() ��
��![]() x��
x��
��S=![]() EFFH=��
EFFH=��![]() x2+
x2+![]() x=��
x=��![]() ��x��1��2+
��x��1��2+![]() ��
��
�൱x=1����EF=1ʱ��S�����ֵΪ![]() ��
��