题目内容
有一个数列{an}是按以下规律组成的:
 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、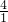 、
、 、
、 、
、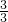 、
、 、
、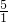 、
、 、…
、…
问:(1) 是数列中的第几项?
是数列中的第几项?
(2)第200项是哪个分数?
解:根据题意分组得: 、(
、( 、
、 )、(
)、( 、
、 、
、 )、(
)、( 、
、 、
、 、
、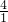 )、(
)、( 、
、 、
、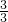 、
、 、
、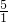 )、
)、 、…
、…
若分子分母相加为n,这组就有n-1个数,
(1)∵50+27=77,∴ 所在组有76个数,
所在组有76个数,
则前一组就有75个数,依此类推前面所有组的数的个数为:1+2+3+4+…+75= =2850,
=2850,
而2850+27=2877,
所以 是数列中的第2877项;
是数列中的第2877项;
(2)1+2+3+4+••+n= ,
,
当n=19时,1+2+3+…+19= =190,
=190,
所以第200项分子、分母之和为21,第200项即为 .
.
分析:此题我们可以看出分子分母相加为n,这组就有n-1个数,
(1)先求出分子分母相加小于76的数的个数,加上27即可得出 在数列中的项数;
在数列中的项数;
(2)先求出n=20时数列{an}的项数为190,200-190=10可得第200项的分子,由于第200项分子、分母之和为21,则第200项为 .
.
点评:本题考查了数字的变化,解题的关键是发现数列{an}中分子分母相加为n的分数有n-1个.
 、(
、( 、
、 )、(
)、( 、
、 、
、 )、(
)、( 、
、 、
、 、
、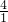 )、(
)、( 、
、 、
、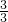 、
、 、
、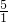 )、
)、 、…
、…若分子分母相加为n,这组就有n-1个数,
(1)∵50+27=77,∴
 所在组有76个数,
所在组有76个数,则前一组就有75个数,依此类推前面所有组的数的个数为:1+2+3+4+…+75=
 =2850,
=2850,而2850+27=2877,
所以
 是数列中的第2877项;
是数列中的第2877项;(2)1+2+3+4+••+n=
 ,
,当n=19时,1+2+3+…+19=
 =190,
=190,所以第200项分子、分母之和为21,第200项即为
 .
.分析:此题我们可以看出分子分母相加为n,这组就有n-1个数,
(1)先求出分子分母相加小于76的数的个数,加上27即可得出
 在数列中的项数;
在数列中的项数;(2)先求出n=20时数列{an}的项数为190,200-190=10可得第200项的分子,由于第200项分子、分母之和为21,则第200项为
 .
.点评:本题考查了数字的变化,解题的关键是发现数列{an}中分子分母相加为n的分数有n-1个.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目