题目内容
下列说法:
①当m>1时,分式 总有意义;
总有意义;
②若反比例函数y= 的图象经过点(
的图象经过点(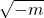 ,
, ),则在每个分支内y随着x的增大而增大;
),则在每个分支内y随着x的增大而增大;
③关于x的方程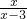 -2=
-2=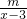 有正数解,则m<6;
有正数解,则m<6;
④在Rt△ABC中,∠ACB=90°,BC=a,AC=b,AB=c,AB边上的高CD=h,那么以 、
、 、
、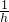 长为边的三角形是直角三角形.
长为边的三角形是直角三角形.
其中正确的结论的个数是
- A.1个
- B.2个
- C.3个
- D.4个
AC
分析:①将x2-2x+m配方,再根据m>1判断分母的符号,
②本题隐含条件为m<0,由k=xy判断k的符号;
③先求解,再根据x>0且x≠3求m的取值范围;
④利用勾股定理的逆定理进行判断.
解答:①∵x2-2x+m=(x-1)2+m-1,∴当m>1时,x2-2x+m>0,分式有意义,结论正确;
②由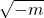 有意义可知,m<0,则k=
有意义可知,m<0,则k=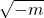 •
• <0,图象在二、四象限,在每个分支内y随着x的增大而增大,结论正确;
<0,图象在二、四象限,在每个分支内y随着x的增大而增大,结论正确;
③解方程得x=6-m,由x>0可得m<6,但x≠3,故m≠3,故应为m<6且m≠3,结论错误;
④依题意,得a2+b2=c2,ab=ch,所以, +
+ =
= =
= =
= ,结论正确;
,结论正确;
正确的有三个.
故选C.
点评:本题考查了勾股定理及其逆定理,分式方程的解,反比例函数图象上点的坐标特点.关键是熟练掌握各知识点的解题方法.
分析:①将x2-2x+m配方,再根据m>1判断分母的符号,
②本题隐含条件为m<0,由k=xy判断k的符号;
③先求解,再根据x>0且x≠3求m的取值范围;
④利用勾股定理的逆定理进行判断.
解答:①∵x2-2x+m=(x-1)2+m-1,∴当m>1时,x2-2x+m>0,分式有意义,结论正确;
②由
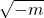 有意义可知,m<0,则k=
有意义可知,m<0,则k=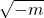 •
• <0,图象在二、四象限,在每个分支内y随着x的增大而增大,结论正确;
<0,图象在二、四象限,在每个分支内y随着x的增大而增大,结论正确;③解方程得x=6-m,由x>0可得m<6,但x≠3,故m≠3,故应为m<6且m≠3,结论错误;
④依题意,得a2+b2=c2,ab=ch,所以,
 +
+ =
= =
= =
= ,结论正确;
,结论正确;正确的有三个.
故选C.
点评:本题考查了勾股定理及其逆定理,分式方程的解,反比例函数图象上点的坐标特点.关键是熟练掌握各知识点的解题方法.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目
 已知函数y=kx+b的图象如图所示,则对于函数y=
已知函数y=kx+b的图象如图所示,则对于函数y=| kb |
| x |
| A、当x增大时,y也增大 |
| B、当x增大时,y减小 |
| C、该函数的图象位于一、三象限 |
| D、该函数的图象位于二、四象限 |
 二次函数y=ax2+bx+c的图象如图所示,给出下列说法中:
二次函数y=ax2+bx+c的图象如图所示,给出下列说法中: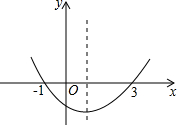 二次函数y=ax2+bx+c的图象如图,给出下列说法:
二次函数y=ax2+bx+c的图象如图,给出下列说法: